
Recall that algorithms like the perceptron look for a separating hyperplane. However, there are many separating hyperplanes and none of them are unique. Intuitively, for an optimal answer, you want an algorithm that finds a hyperplane that maximizes the margin between different classes so that it can perform better on new data. Support Vector Machines (SVM) accomplishes this and finds a unique hyperplane by solving the primal and dual problem. SVMs can also be extended to classify non-linearly separable data by using soft margin classification and implicitly mapping inputs into high-dimensional feature spaces to classify them easier using the kernel trick.
You're Naruto Uzumaki (a ninja). It's you and your team's job to get an important person to other side of the land, safely and as comfortably as possible. There is an army of Hidden Mist ninjas on the right and an army of Sand ninjas on the left trying to kill the important person. In addition to making it to the other side of the land, the important person also has a personal goal of predicting whether a ninja is a Hidden Mist ninja or a Sand ninja.

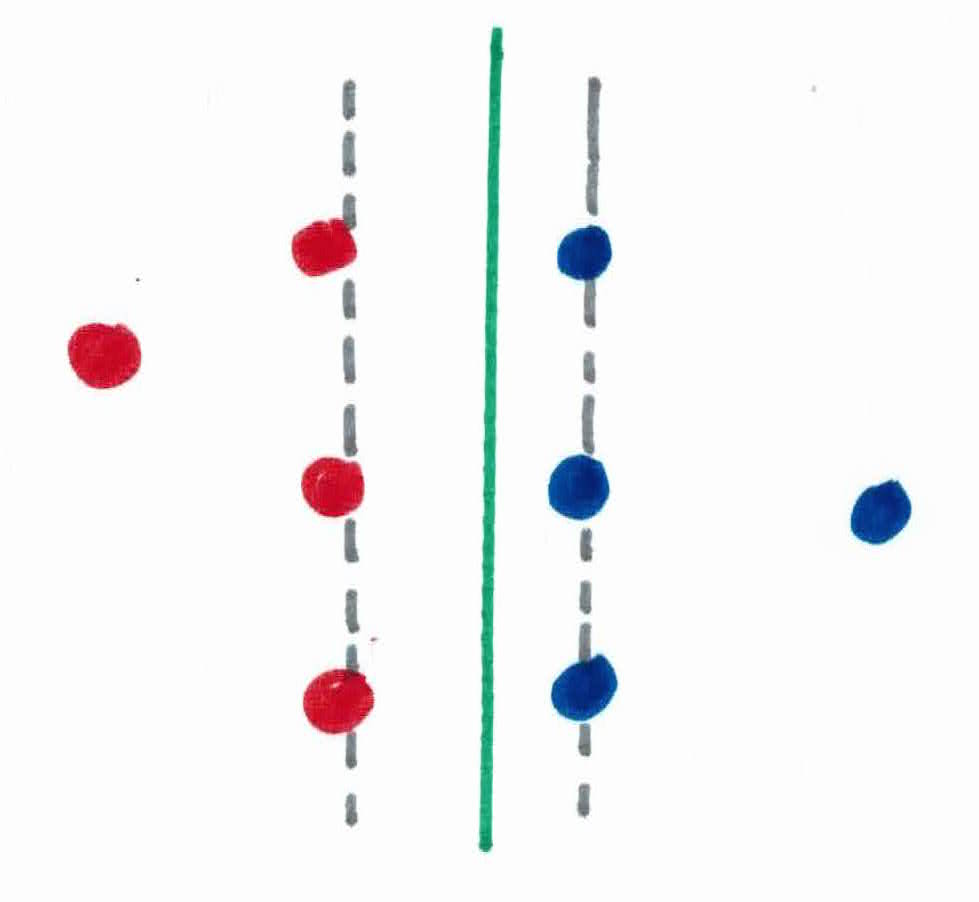
In order for you to protect him, you use your jutsu (magic powers) to set up 2 straight rock barriers on your left and right, between the important person and the 2 armies. There are many ways to do this, as you can see:
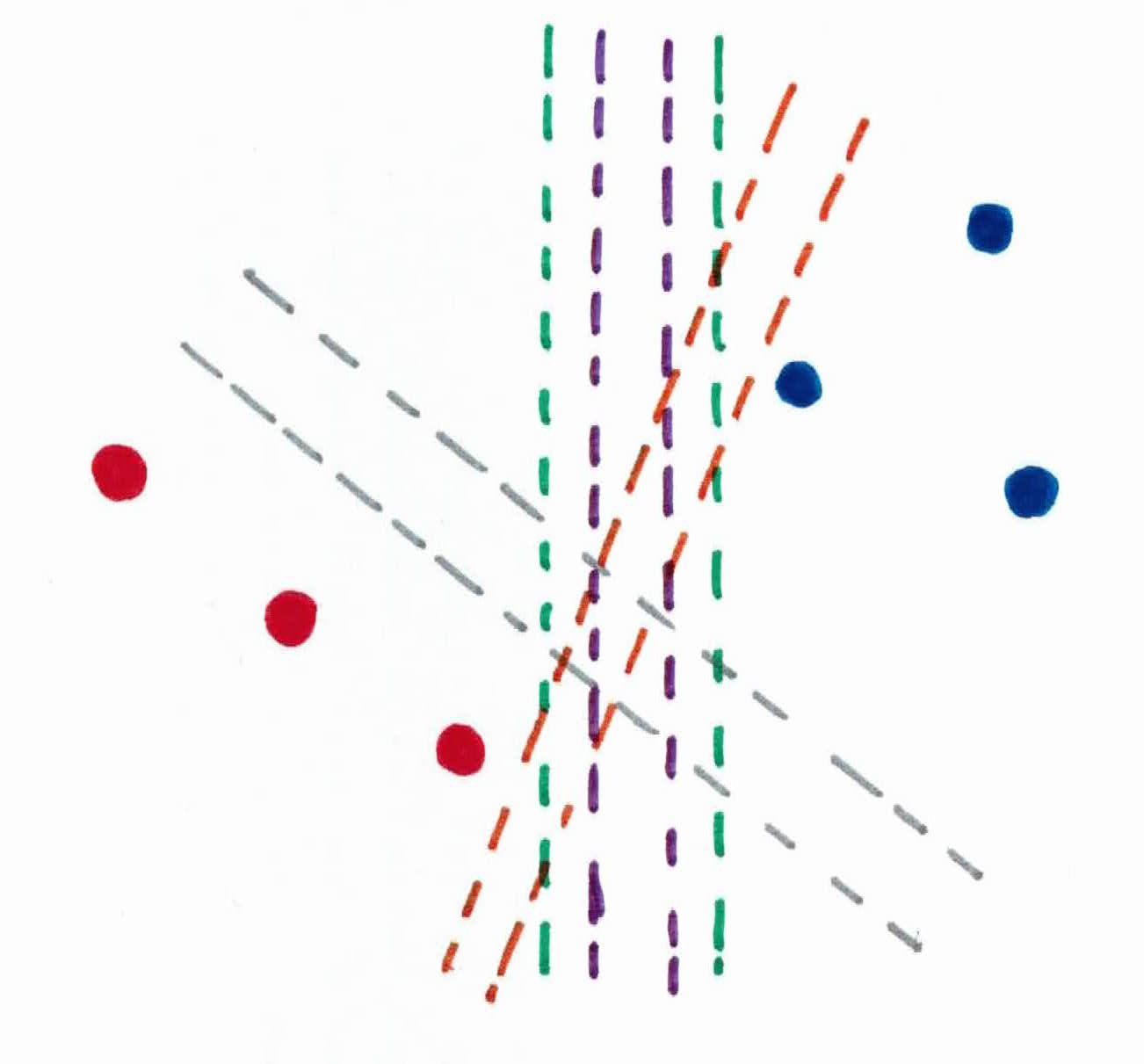
But you want the important person to be safe, and comfortable. In order to do this, you must give him the most space possible to walk. This is accomplished by maximizing the margin between the the Hidden Mist ninjas and the Sand ninjas, allowing the important person to walk exactly in the middle of the 2 barriers.

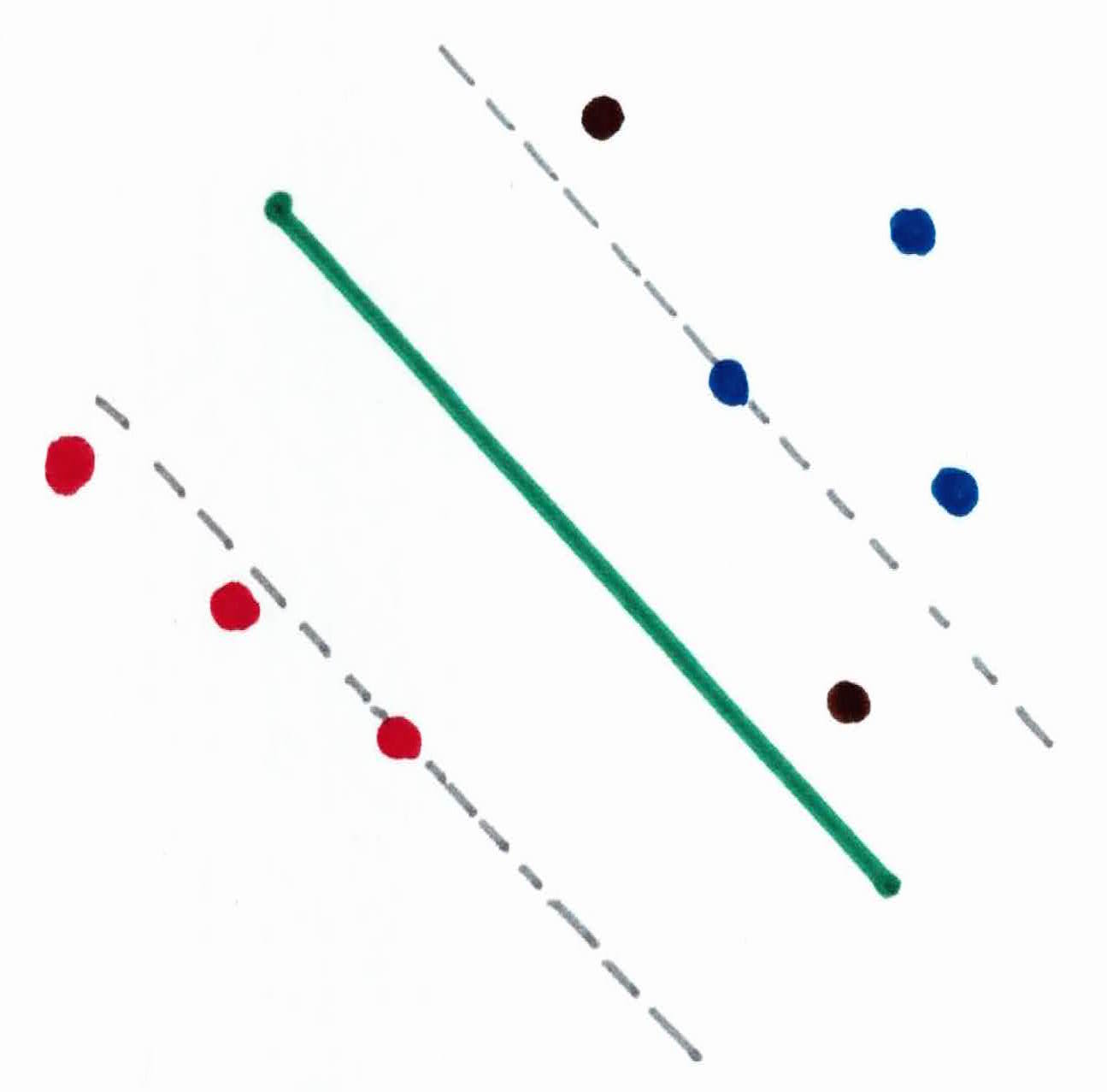
So, naruto uses his jutsu to build two parallel rock barriers, making the margin as big as possible. The first wall will be placed on the left, stopping the Hidden Mist, and the and the second wall will be placed on the right, stopping the Sand. The Hidden Mist and Sand ninjas that the respective walls made contact with are known as support vectors.

The important person now walks safely to his destination, dead in the center of the two walls. His path of walking is known as the hyperplane. Any new ninja to the right of his walking path, he predicts will be a Hidden Mist ninja, whether they are within the walls or not. And the same goes for the left and the Sand ninja. However, you are extremely confident with your prediction if a new ninja appears on the other side of the walls (support vectors).
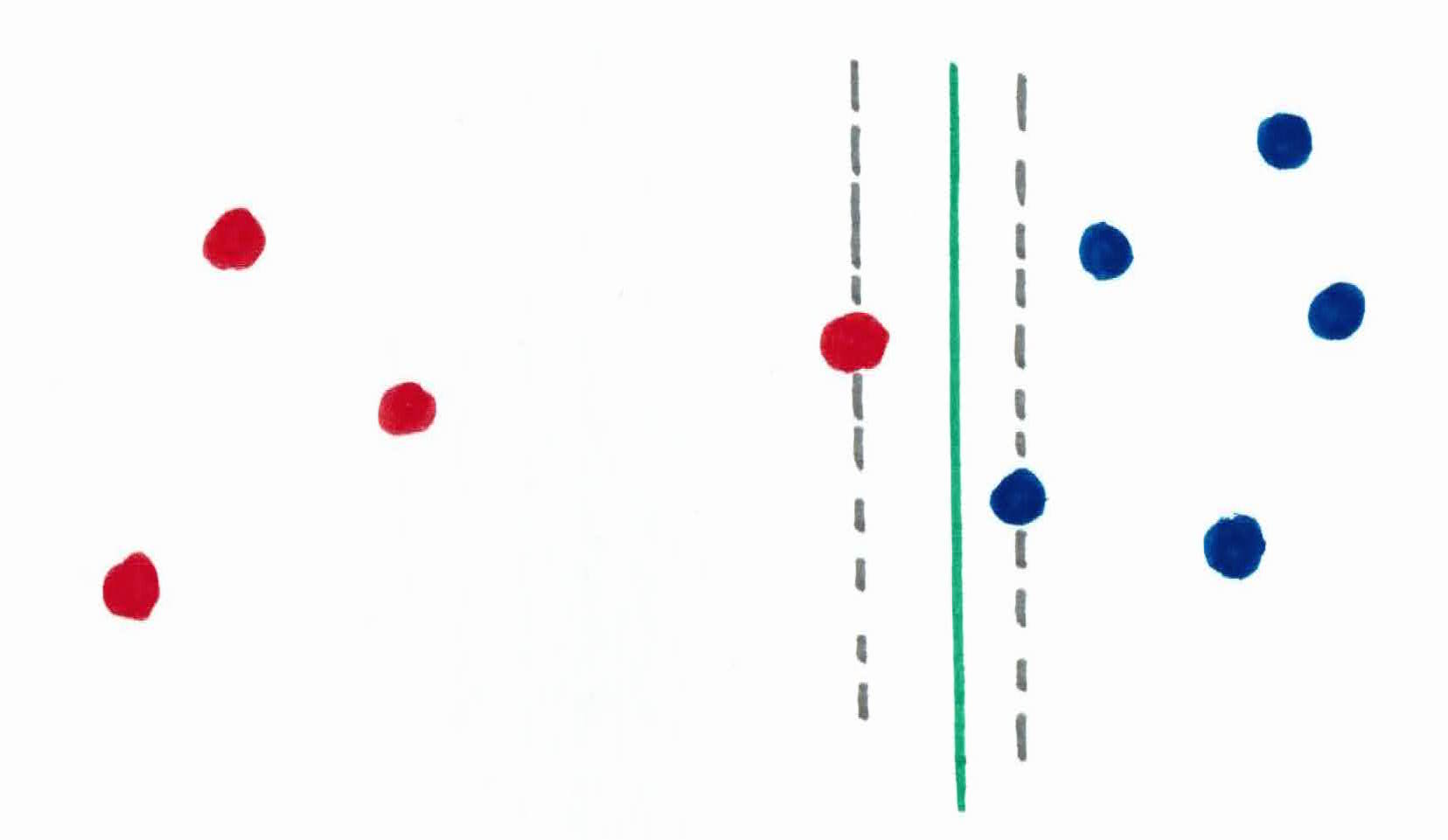
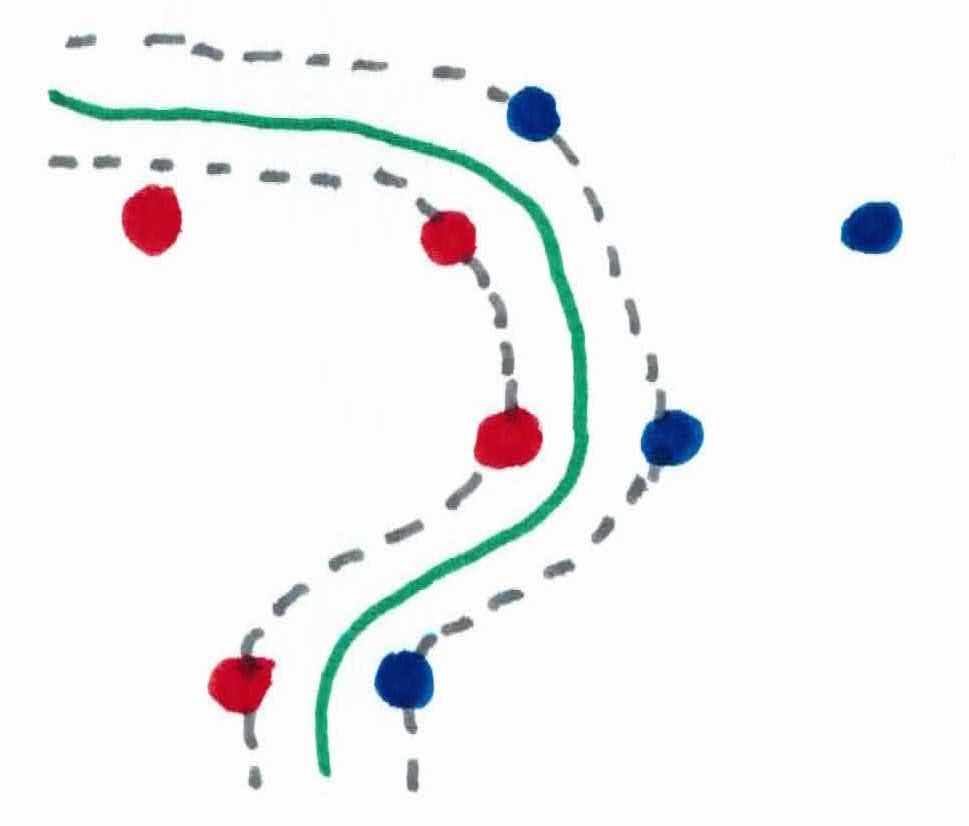
There are also cases where a few ninjas are ruthless and are closer in together, attacking more aggressively. If you were to build the walls using your justsu to block all ninjas like before, you run the risk of forcing yourself to make narrow walls, and making the important person extremely uncomfortable, walking through a tight space. Narrow walls will also make the important person less confident in his predicted answers.
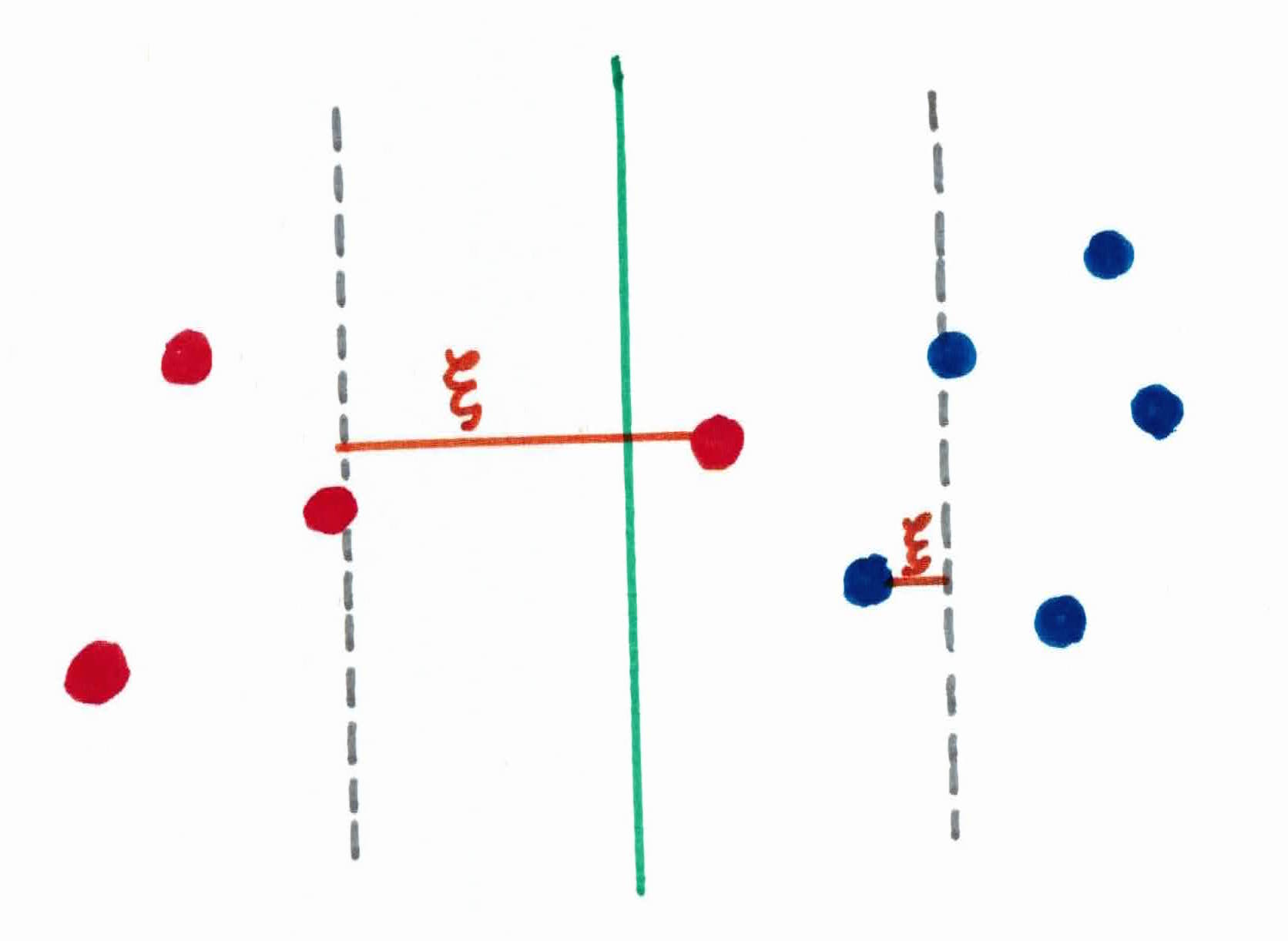
So, what you could do, is allow a few of those outlier ninjas in the area, while still making a large margin. The tradeoff is that now the important person is caught of guard, and isn't able to predict which ninja is which. There will be some damage $\xi$ taken, there is no free lunch. This is called soft margin classification.
In the final case, all the ninjas are grouped together, attacking from all angles. The important person must still make it to the other side of the village, and still wants to predict accurately where each ninja is. The issue is, the threats are not linearly separable. At least not in 3 dimensions.

So, Naruto uses his special Sage Genjustu skills to project everyone into 5 dimensions. In 5 dimensions, the ninjas are placed in different spots. The world looks different.

He is able to make linear walls in 5 dimensions to separate them.
In 3 dimensions it seems non-linear, but in 5 it is linear. The special Sage Genjustu he used to implicitly move everyone into 5 dimensions is known as the kernel trick.
Recall that most algorithms model situations by creating a feature space, which is a finite-dimensional vector space, where each dimension represents a feature of your training examples.
For example, if you wanted to classify whether someone was an adult or child (labels), and you were given 2 features (height and weight), you would model it with a 2 dimensional graph. In order to classify, you want to find a a hyperplane that will separate the data. So, when you get new data you want to classify, you just simply see what side of the hyperplane that new piece of data falls on.
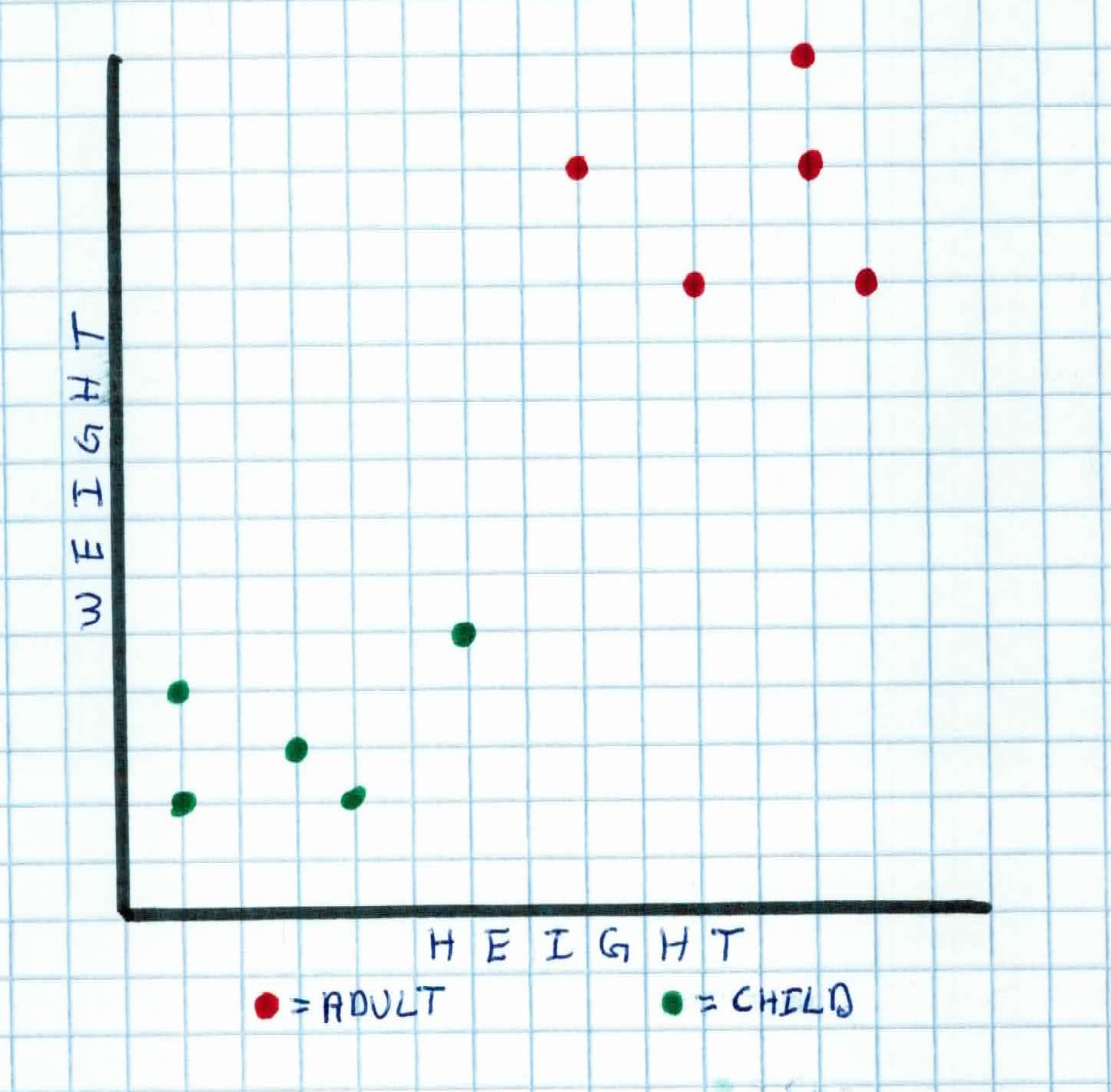
Support Vector Machines (SVM), unlike the perceptron, finds the most optimal separating plane with the largest margin between classes. We want to look for a hyperplane that maximizes the space between both classes, because if we select a hyperplane which is close to the data points of one class, then it might not generalize well to new, unseen data. When we get more data points, if the margin was maximized, there is a smaller chance that the new data point will be placed on the wrong side of the hyperplane. So we want a hyperplane that is as far as possible from data points from each category.
SVMs have the most math out of any of the other algorithms that you have seen thus far. So, I will first walk you though what we will be doing:
Given a particular hyperplane, we can compute the distance between the hyperplane and the closest data point. Once we have this value, if we double it, we will get what is called the margin.
To compute the margin, we have to have a working knowledge of how to find the sum/difference, magnitude, unit vector, and dot product of vectors (click the links to learn/refresh).
Recall that an equation of a line is usually written as $y=ax+b$. However, in machine learning literature, you usually see the equation of a hyperplane defined as:
$$w^Tx +b = 0$$
where $\ w \in \mathbb{R}^d, \ x \in \mathbb{R}^d, \ b \in \mathbb{R}$.
These two equations are the same thing. $b$ is simply the bias which means that this value determines the intersection of the line with the vertical axis.
We use $w^T x=0$ because it is easier to work in two dimensions with this notation and the vector $w$ will always be orthogonal to the hyperplane (because two vectors are orthogonal if their dot product is zero).
Let's show an example. We set $b = 0$, so it will pass through the origin:
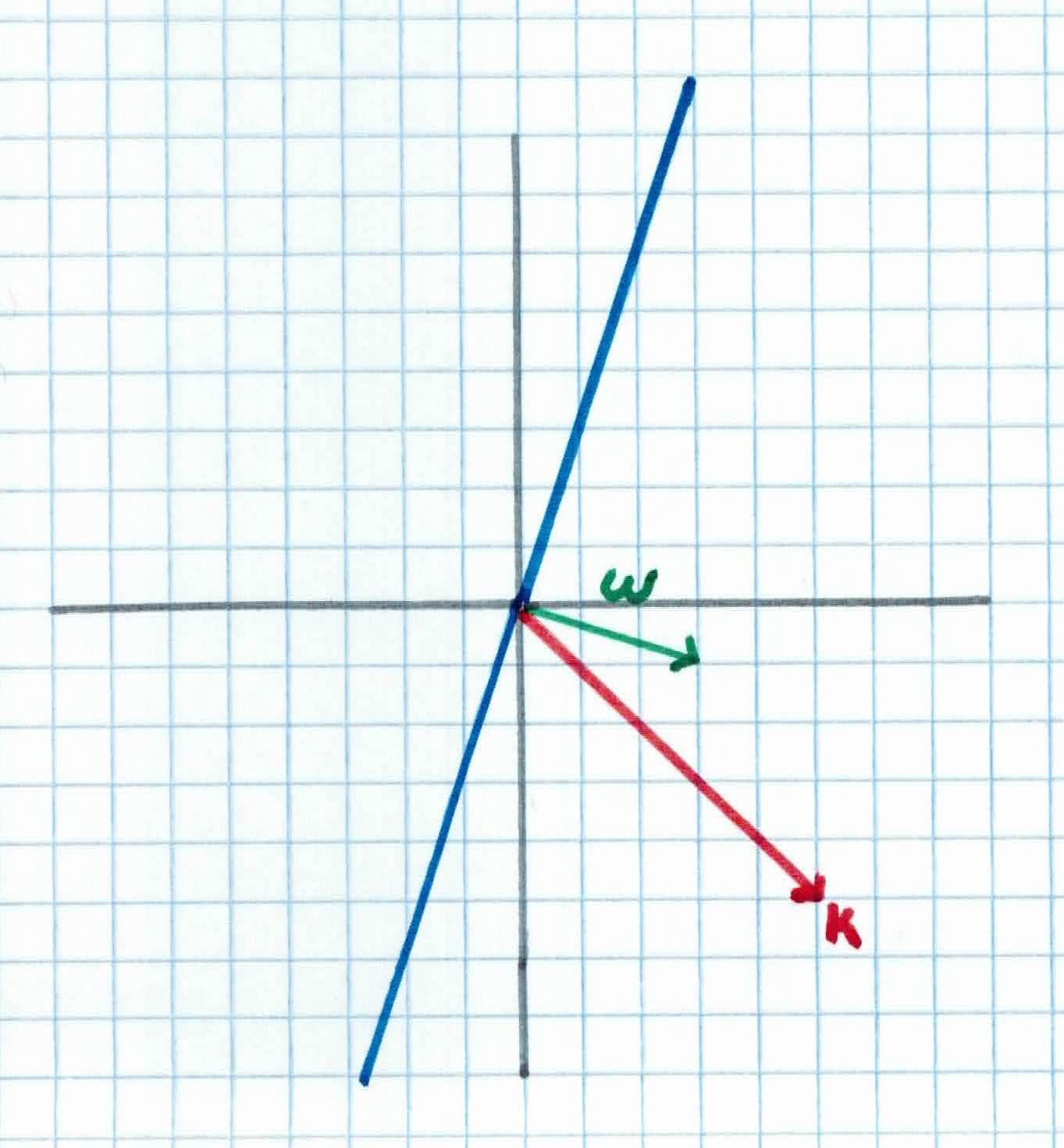
As you can see, the equation of the hyperplane is:
$$x_2 = 3x_1$$
$$=w^Tx = 0$$
with $w= \left ( \begin{array}{c} 3 \ -1 \end{array} \right)$ and $x=\left ( \begin{array}{c} x_1 \ x_2 \end{array} \right)$
We would like to compute the distance between the closest point $K=(5,-5)$ and the hyperplane. You can find this by finding the magnitude of the projection of $K$ on the weight vector $w$. We can view the point $K$ as a vector from the origin to $K$. If we project it onto the normal vector $w$ we get vector $P$.
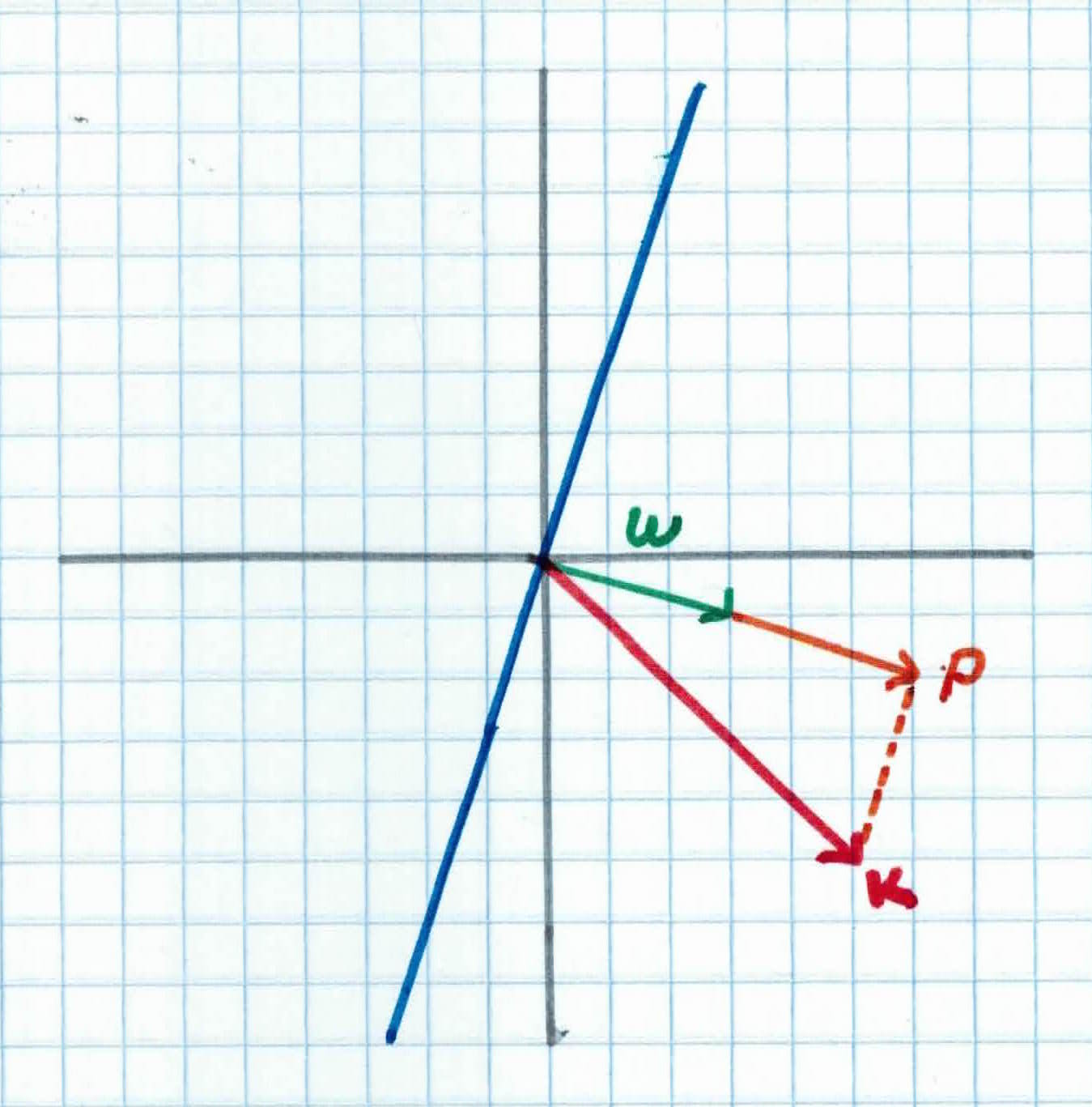
Recall that the orthogonal projection formula of $K$ onto $w$ is given by:
$$proj_{w}K = \frac{K^Tw}{||w||^2}w$$
We start with two vectors, $w= (3,-1)$ which is normal to the hyperplane, and $K=(5,-5)$ which is the vector between the origin and $K$.
Our projection vector is given as:
$$P = \frac{K^Tw}{||w||^2}w$$
$$K^Tw = 3 \times 5 + (-1) \times (-5) = 20$$
$$||w||^2 = \sqrt{3^2 + (-1)^2}^2=\sqrt{10}^2 = 10$$
$$\frac{K^Tw}{||w||^2} =\frac{20}{10}= 2$$
$$P = \frac{K^Tw}{||w||^2}w= 2\times(3,-1) = (6, -2)$$
So, $P=(6,-2)$, and it's distance/magnitude is given by:
$$||P|| = \sqrt{6^2 + (-2)^2} = 2 \sqrt{40}$$
Now that we have the distance $P$ between $K$ and the hyperplane, the margin is defined by:
$$margin = 2 \times ||P|| = 2 \sqrt{40}$$
We have computed the margin of the hyperplane. But how do we find the optimal hyperplane? We form the primal problem.
After selecting two hyperplanes which separate the data with no points between them, you maximize their distance (margin) and the region bounded by the two hyperplanes will be the biggest possible margin.
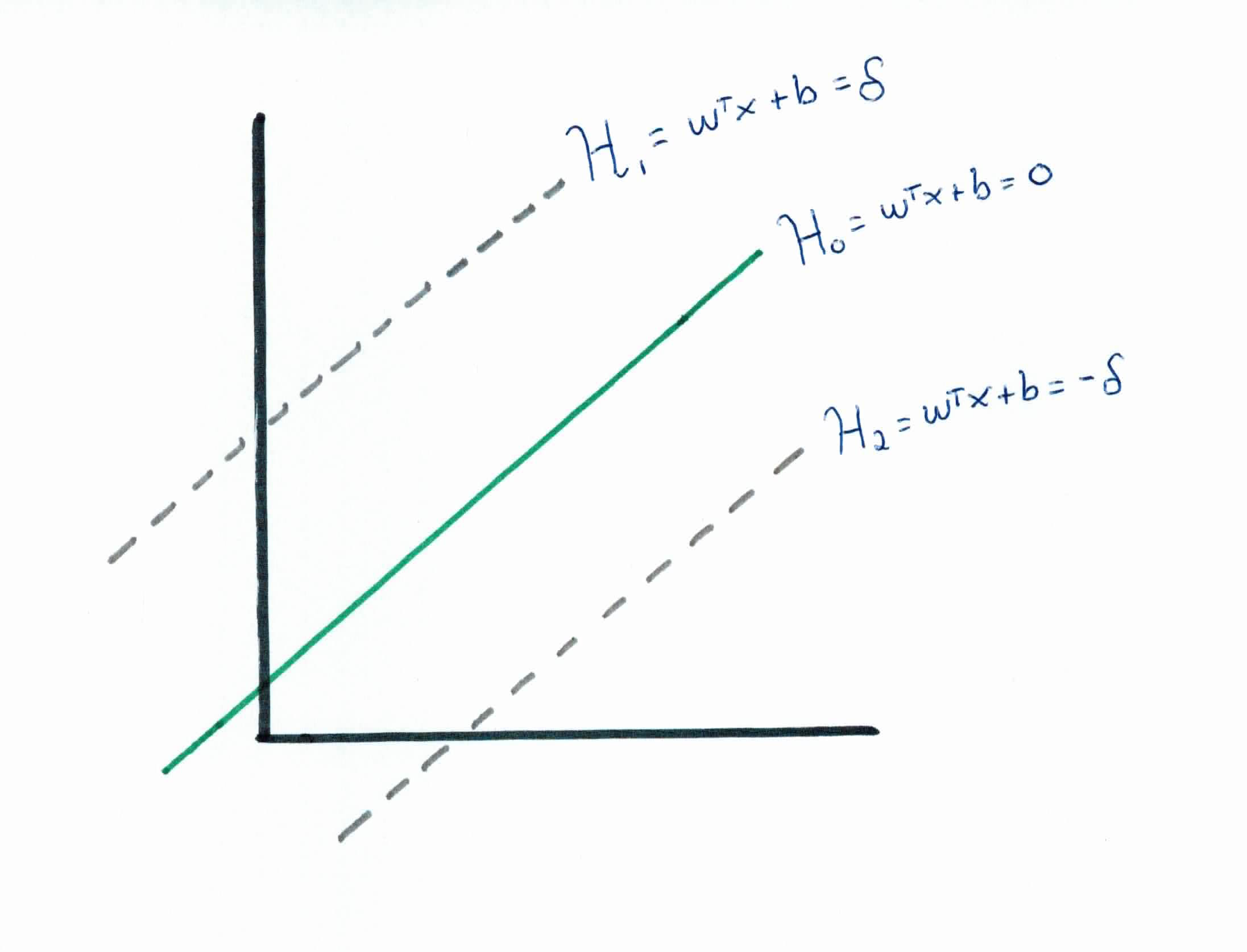
Given a hyperplane $\mathcal{H}_0$ separating the dataset and satisfying:
$$w^Tx + b = 0$$
We can select two other hyperplanes $\mathcal{H}_1$ and $\mathcal{H}_2$ which also separate the data and have the following equations:
$$w^Tx + b = \delta$$
and
$$w^Tx + b =-\delta$$
so that $\mathcal{H}_0$ is equidistant from $\mathcal{H}_1$ and $\mathcal{H}_2$.
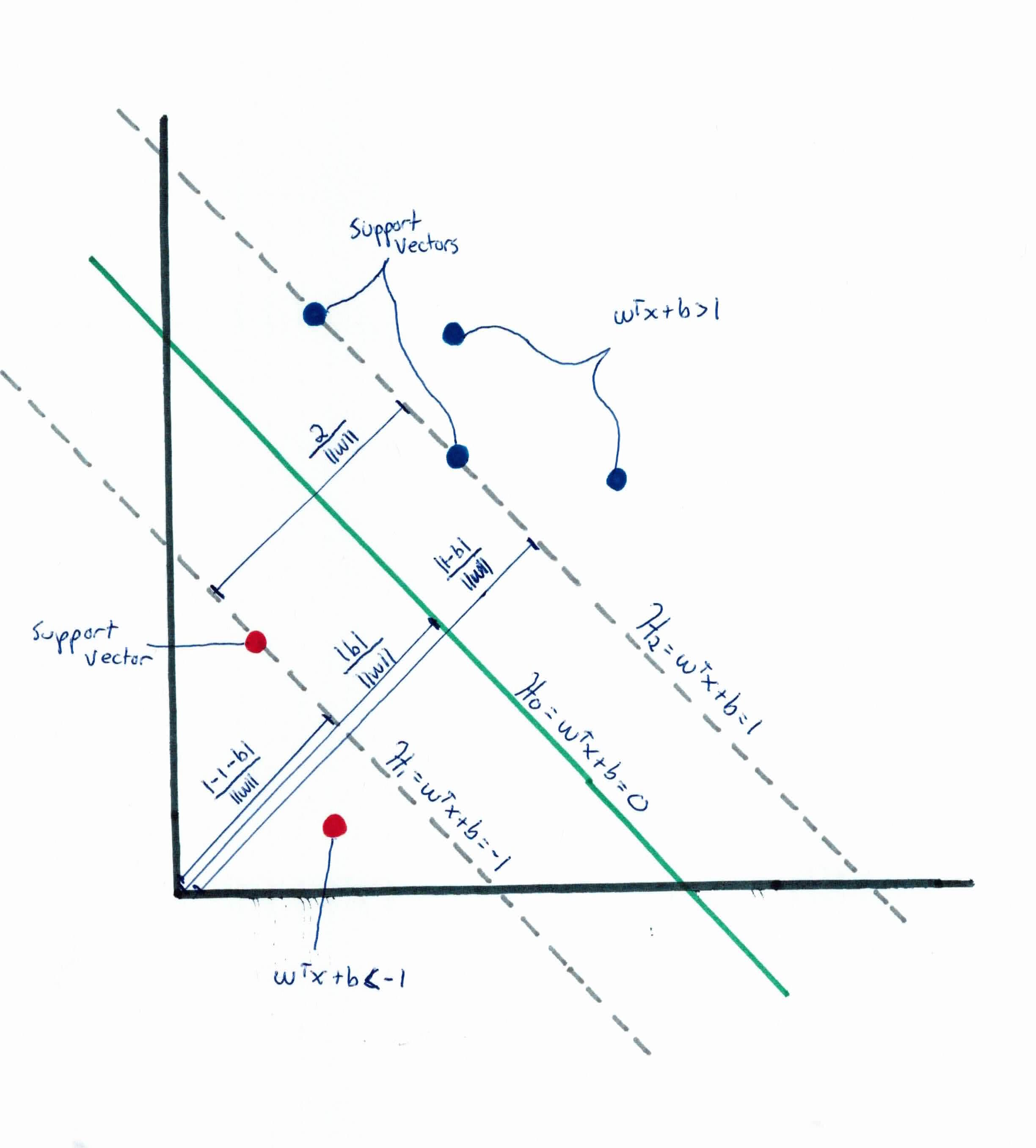
Note that from the Point-Plane Distance formula, we get that $\frac{\mid b \mid}{\|w\|}$ is the perpendicular distance from the hyperplane $\mathcal{H}_0$ to the origin.
When tuning parameters, we just need to alternate one. So we can simplify the problem by setting $\delta = 1$, so now we have:
We want to make sure (try) to have no points between them. We won't select just any hyperplane, we will only select those who meet the two following constraints:
For each training example vector $x_i$ for all $1 \leq i \leq n$ either:
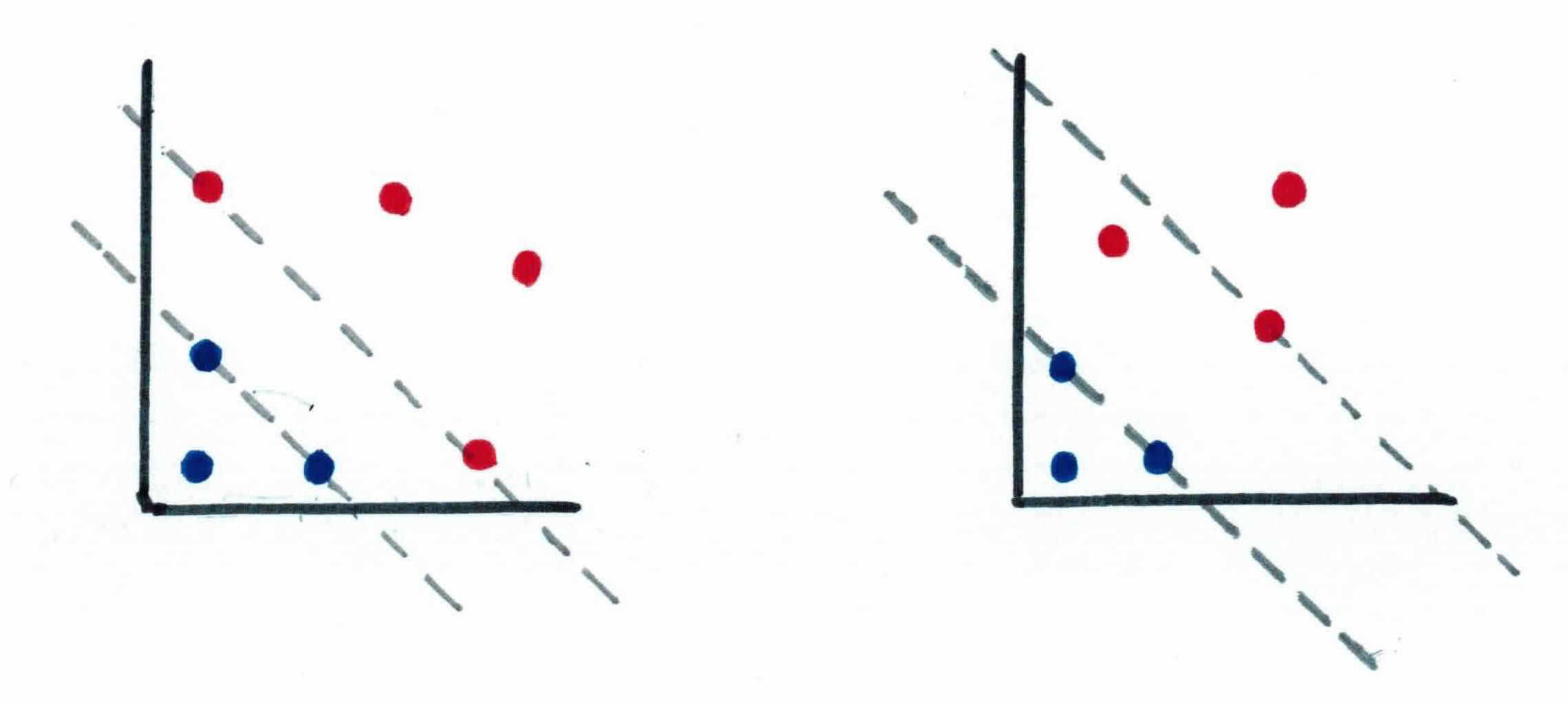
To express this more compactly, we can put them together into a single constraint:
$$y_i(w^T x_i + b) \geq 1 \ for \ all \ 1 \leq i \leq n$$
This is true because the output is a discrete answer i.e. $ y_i = { -1, +1 }$ for a positive example or negative example.
Earlier, for uniqueness, recall that we set $\mid w^Tx + b\mid = 1$ for any example $x_i$ closest to the boundary. So, the distance from the closest sample $x_i$ to $w^Tx+b = 0$ is:
$$\frac{\mid w^Tx+b\mid}{\|w\|}=\frac{1}{\|w\|}$$
We then double it and have the margin is $\frac{2}{\|\mathbf{w}\|}$. As you can see, if we want to make the margin bigger, we must minimize $\|\mathbf{w}\|$. The smaller $\|\mathbf{w}\|$ is, the bigger the margin.
Therefore, we will try to minimize $\frac{1}{2}\|w\|^2$ such that $y_i(w ^T x_i + b) \geq 1$ for all $1 \leq i \leq n$. We added the $\frac{1}{2}$ and squared it to make it more mathematically easy. We do this a lot in mathematics.
This results in the following constraint optimization problem known as the primal problem:
$$min\frac{1}{2}\|w^2\|$$
$$Subject \ to \ y_i (w^Tx + b) \geq 1 \ for \ all \ 1 \leq i \leq n$$
Don't forget what the purpose of doing this is. We want to minimize (w) to increase the margin. However, the margin must respect the constraints we set, so we can find the largest margin that separates all classes.
Solving this equation is no different than solving a homework assignment in Calc 3 class. Once this is solved, we have found the parameters for which $\|w\|$ is the smallest possible and the constraints we fixed are met. Which means we will have the equation of the optimal hyperplane!
The primal form, which is an optimization problem with a convex quadratic objective and linear constraints, can be solved using commercial quadratic programming (QP) code.
Although it seems that we have solved the problem, we will make a digression to talk about Lagrange Duality. This will lead us to our optimization problem’s dual form. In the primal problem, in order to classify a new point, we must explicitly compute the scalar product $w^Tx_i$ which may be expensive if there are a lot of features (high dimensions). The dual form, however, will be easier to compute and play a key role in allowing us to work efficiently in very high dimensional spaces.
In order to move on, you must be comfortable with partial derivatives, gradient, hessian, and convex functions.
In mathematical optimization theory, duality means that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem (duality principle). The solution to the dual problem provides a lower bound to the solution of the primal (minimization) problem. It turns out that most times, solving the dual problem is simpler than solving the primal problem.
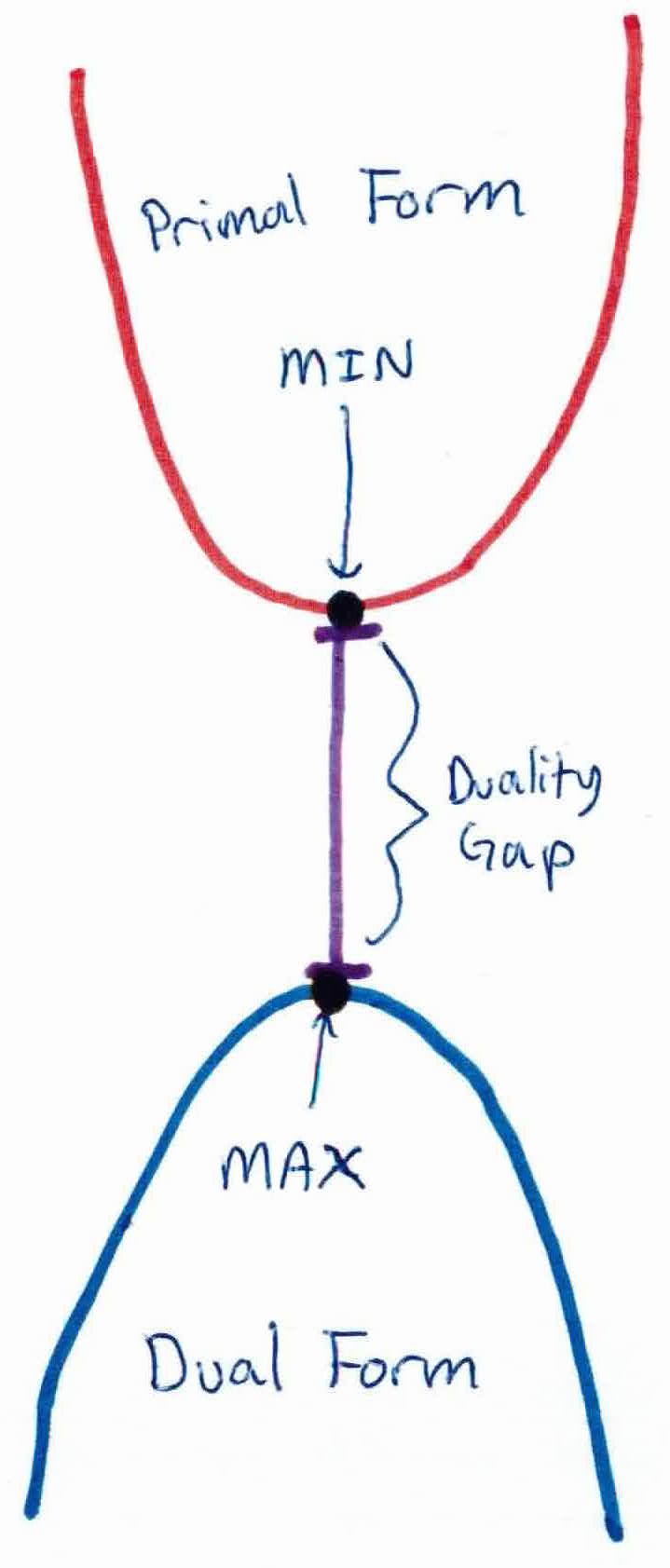
In the schema above, imagine that in our primal problem, we are trying to minimize the function at the top of the graph. Its minimum is the black dot at the bottom of the primal. If we search for a dual function, we could end up with the one at the bottom of the graph, whose maximum is the black dot at the top of the dual. In this case, we clearly see that dual black dot is a lower bound. We call the value $ primal_{dot}-dual_{dot}$ the duality gap. In this example, $ primal_{dot}-dual_{dot} > 0$ and we say that weak duality holds.
For strong duality to hold, there must be no duality gap, i.e. $primal_{dot}-dual_{dot}=0$. This is when the solution to both primal and dual will be the same. It is shown below:
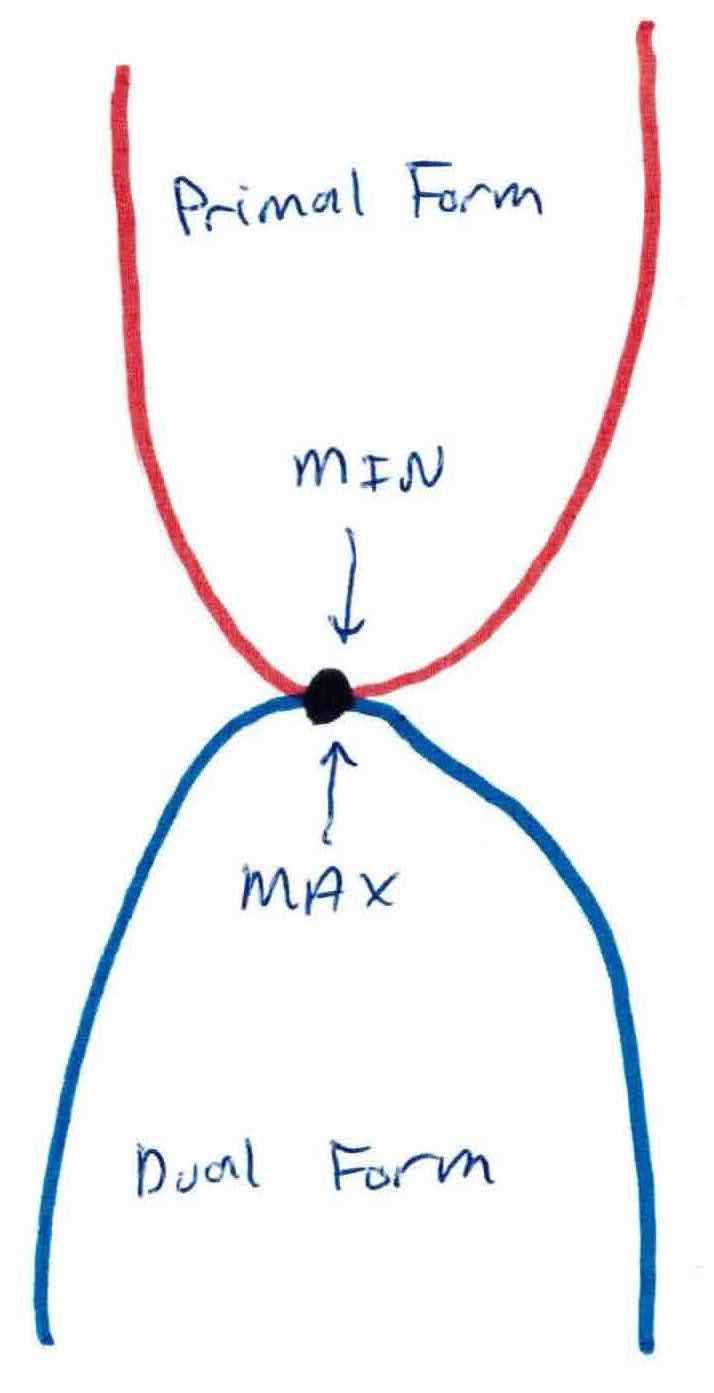
Dual and primal could give us the same answer. The reason we'd rather solve the dual is because we will be able to use kernels. Keep reading below.
Recall from above that in constraint problems, an optimization problem is typically written as:
$$\left. \begin{array}{rcl} \mathsf{minimize}_w & f(w) \\ \mathsf{subject \ to} & g_i(w) \leq 0, \ \ \ i = 1, \ldots, k\\ & h_i(w) = 0, \ \ \ i =1, \ldots, l \end{array} \right. $$
where there are $k$ functions $g_i$ which define inequality constraints and $l$ functions $h_i$ which define equality constraints.
For instance, if I said:
$$\left. \begin{array}{rcl} \mathsf{minimize}_x & x^2 \\ \mathsf{subject \ to} & x \geq 1 \\ & x \leq 2 \end{array} \right. $$
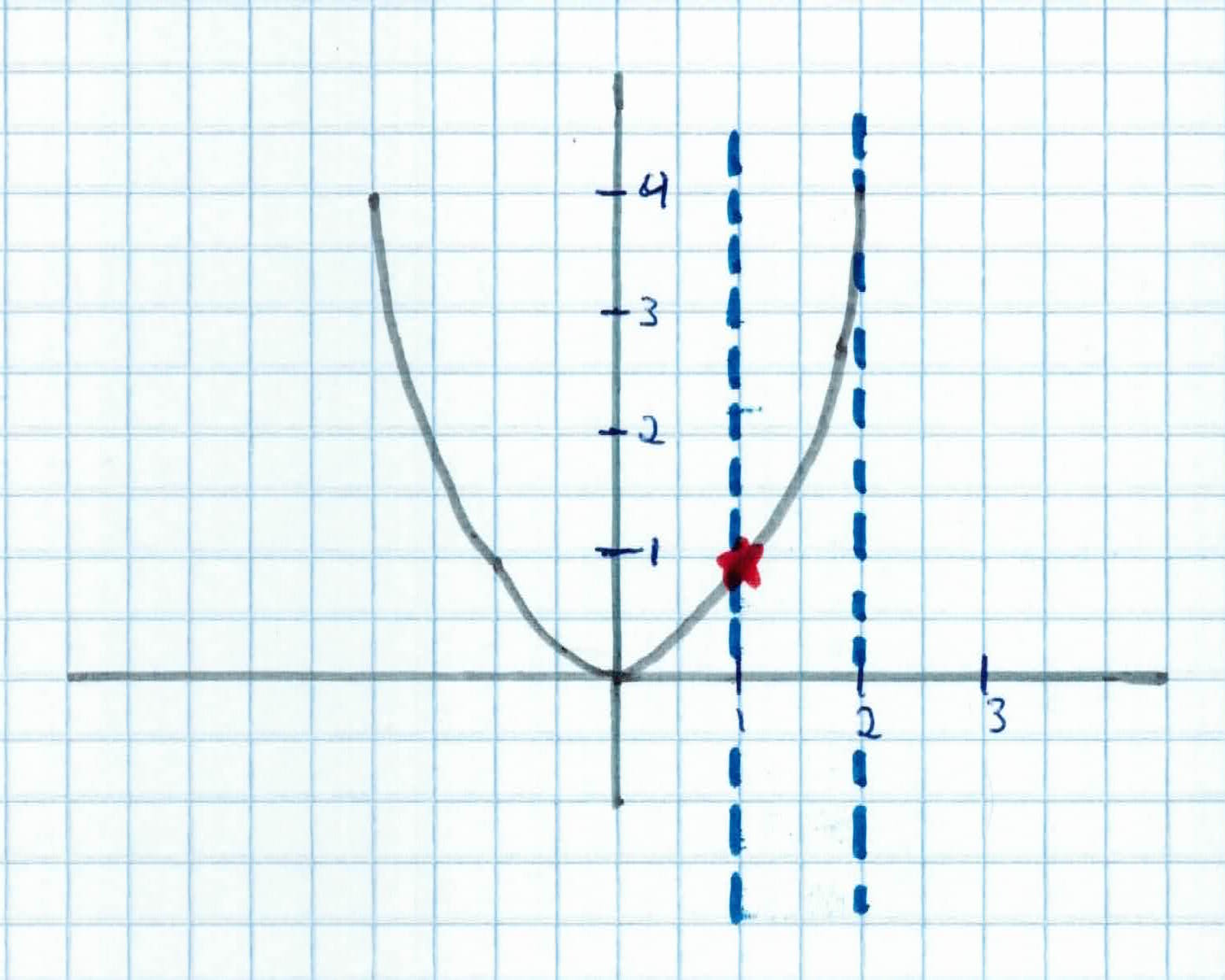
The red star would be our optimal point in, which is within the constraints.
So what's one way we can find a solution to the optimization problem? We use can use Lagrange Mulitipliers! In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equality/inequality constraints. More on Lagngrangian here.
So our Generalized Lagrangian has the form:
$$\left. \begin{array}{rcl} \mathsf{Argmin}_w & f(w) \\ \mathsf{subject \ to} & g_i(w) \leq 0, \ \ i = 1, \ldots, k\\ & h_i(w) = 0, \ \ i =1, \ldots, l \end{array} \right. $$
$$\mathcal{L} (w, \alpha, \beta) = f(w) + \sum_{i=1}^k \alpha_i g_i(w) + \sum_{i=1}^l \beta_i h_i(w)$$where $g$, $h$ are the constraints our function is subject to and $\alpha$, $\beta$ are our Langrange multipliers. We would then find and set $\mathcal{L}$'s partial derivatives to zero to solve for the parameters we are looking for.
Solution $w^*$ is the optimal $w$ in the primal, $\alpha^*$ and $\beta^*$ are the optimal $\alpha$ and $\beta$ in the dual.
For a solution to exist (and hence the primal and dual problems are equivalent), the Krush-Kuhn-Tucker Conditions (KKT) must be fulfilled.
Moreover, if some $w^*$, $\alpha^*$, and $\beta^*$ satisfy the KKT conditions, then it is also a solution to the primal and dual problems, i.e. Primal $=$ Dual $=\mathcal{L}(w^* \alpha^*, \beta^*)$.
So, going back to our original (primal) problem:
$$min\frac{1}{2}\|w^2\|$$
$$Subject \ to \ y_i (w^Tx + b) \geq 1 \ for \ all \ 1 \leq i \leq n$$
where we can write the constraints as:
$$g_i(w) = -y_i(w^Tx_i + b)+1 \leq 0$$
If we try to set it up as a Lagrangian, we get:
$$\mathcal{L} = \frac{1}{2} w^Tw + \sum_{i=1}^n \alpha_i (1-y_i(w^Tx_i + b))$$
with $$\|w\|^2 = w^Tw$$
Note that there are no $\beta_i$ Lagrange multipliers, since the problem only has inequality constraints.
Setting the derivatives of $\mathcal{L}$ w.r.t $w$ and $b$ to zero, we have:
$$\bigtriangledown_w \mathcal{L}=w + \sum_{i=1}^n \alpha_i (-y_i)x_i = 0$$
$$w = \sum_{i=1}^n \alpha_i y_i x_i$$
and
$$\frac{\partial \mathcal{L}}{\partial b} = \sum_{i=1}^n \alpha_iy_i = 0$$
By plugging in these 2 quantities back into Lagrangian $\mathcal{L}$, we get:
$$\mathcal{L}(w, \beta, \alpha) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j = 1}^n y_i y_j \alpha_i \alpha_j x_i^T x_j- b \sum_{i=1}^n \alpha_i y_i$$
But recall that from partial derivatives of $b$, the last term must be zero, so after simplifying, we obtain:
$$\mathcal{L}(w, \beta, \alpha) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i = 1}^n \sum_{j=1}^n y_i y_j \alpha_i \alpha_j x_i^T x_j$$
Recall that we got to the equation above by minimizing $\mathcal{L}$ with respect to $w$ and $b$. Putting this together with the constraints $\alpha_i \geq 0$ (that we always had) and the constraint from taking the partial derivative of $b$, we obtain the following dual optimization problem:
$$max_\alpha \ W(\alpha) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n y_i y_j \alpha_i \alpha_j x_i^T x_j$$
such that $ \alpha_i \geq 0, \ i =1, \ldots, n$ and
$$\sum_{i=1}^n \alpha_i y_i = 0$$
The objective function of the dual problem needs to be maximized and can be done with QP solvers. Solve the dual problem to find the $\alpha^*s$. Once we find the $\alpha^*s$, we can find the optimal $w$'s with:
$$w^* = \sum_{i=1}^n \alpha_i^* y_ix_i$$
Having found $w^*$, by considering the primal problem, it is also straightforward to find the optimal value for the intercept term $b$:
$$b^* = -\frac{max_{i:y_i=-1}w^{*T}x_i + min_{i:y_i=1}w^{*T}x_i}{2}$$
Then, for a new data $z$, we can make a prediction simply by computing:
$$w^Tz + b = \sum_{i=1}^n \alpha_{i}^*y_{i}x_i^Tz+b^*$$
and classify $z$ as class 1 if sum is positive and class 2 otherwise.
You will see that all of the $\alpha$'s besides the support vectors will be zero. There are only a small number of support vectors and the decision boundary is determined only by them. As a result, many of the terms in the sum above will be zero, so we will only need to find the inner products between $z$ and the support vectors in order to calculate and make our prediction.
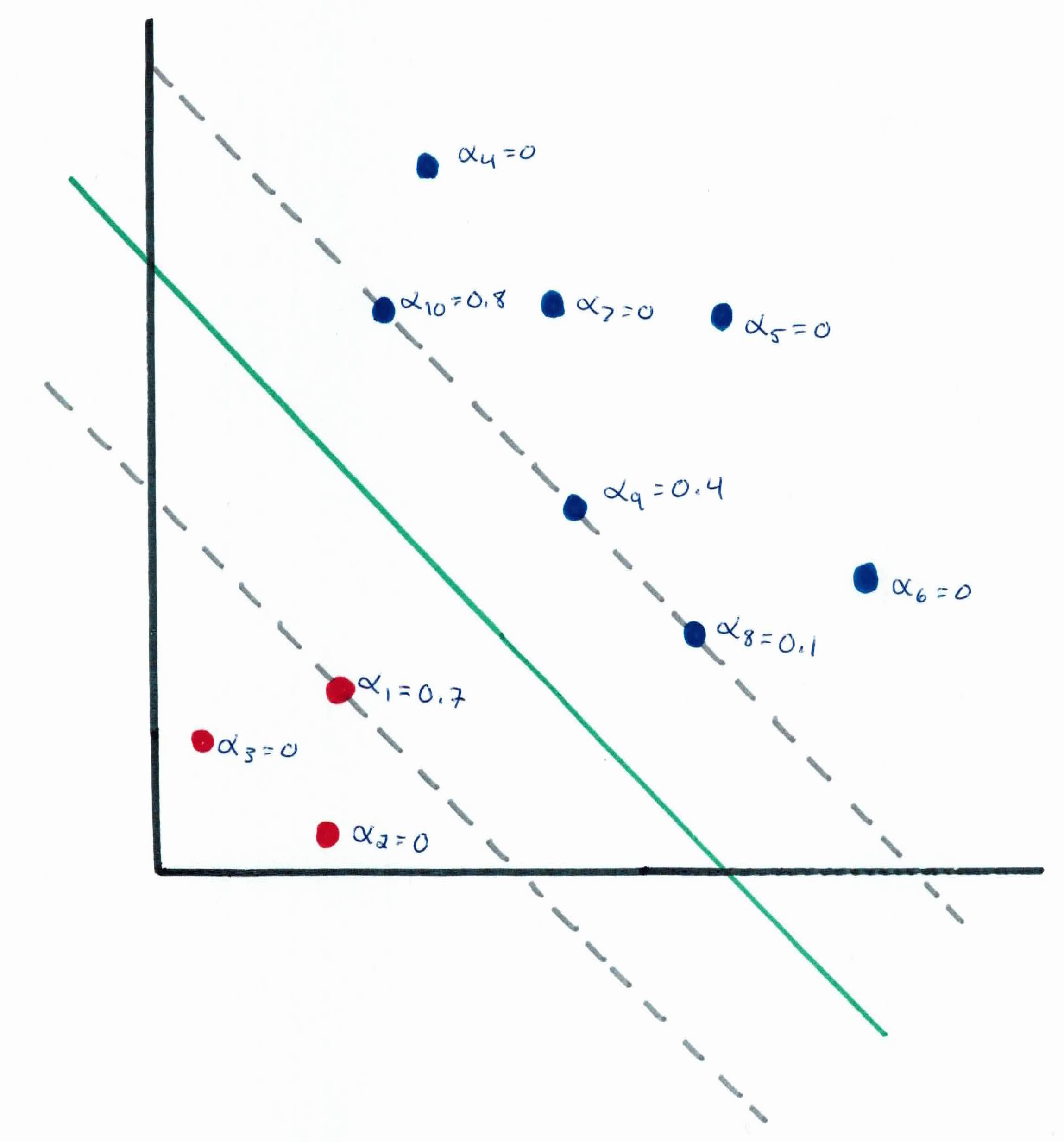
By examining the dual form of the optimization problem, we were able to write the entire algorithm in term of only inner products between input feature vectors. We will later exploit this property to apply kernels to be able to efficiently learn in very high dimensional spaces.
What about for non-linearly separable data? We use a soft-margin hyperplane. We allow some small error $\xi_i$ in classification so that we can still maximize the margin and generalize better for unseen data. $\xi_i$ are slack variables in optimization and they approximate the number of misclassified samples:
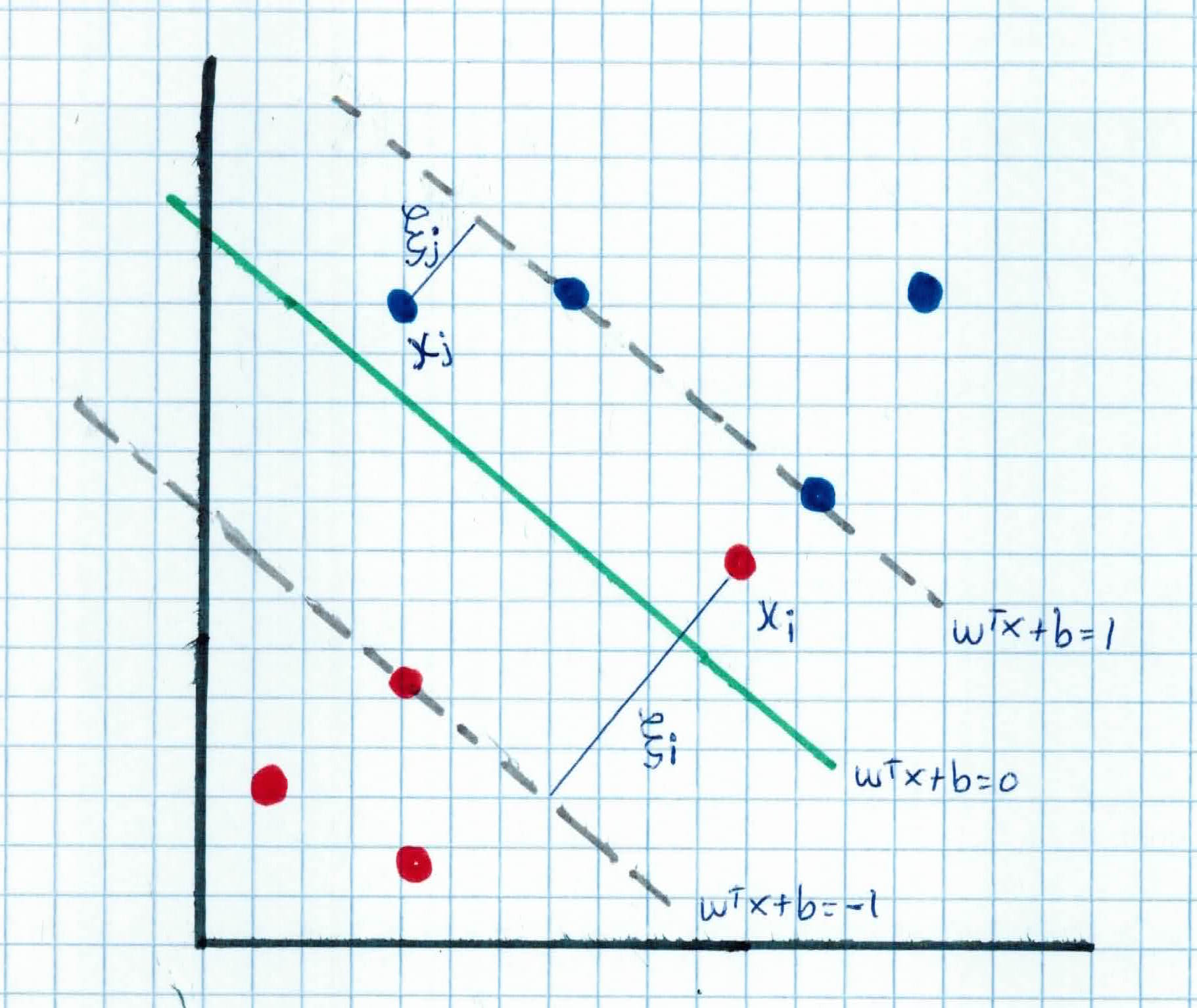
Once we account for slack variable $\xi$, we get:
$$\left. \begin{array}{rcl} w^Tx_i + b \geq 1 - \xi_i & y_i = 1 \ w^Tx_i + b \leq -1 + \xi_i & y_i = -1 \ \xi_i \geq 0 & \forall i \end{array} \right.$$
As you can see, we want to minimize $\frac{1}{2} \|w\|^2 + C \sum_{i=1}^n \xi_i$ where $C$ is tradeoff parameter between error and margin. A large $C$ corresponds to assigning a higher penalty to errors. Note that if $\xi_i = 0$ there is no error in $x_i$. You can think of $\xi_i$ as an upper bound of the number of errors.
The optimization problem then becomes:
$$ Argmin_{w,b} \frac{1}{2} ||w||^2 + C \sum_{i=1}^n \xi_i $$
$$subject \ to \ y_i(w^Tx_i +b) \geq 1 - \xi_i$$
$$\xi_i \geq 0 \ for \ all \ 1 \leq i \leq n$$
The dual of this new constrained optimization problem is:
$$Argmax_\alpha W(\alpha) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j x_i^T x_j$$
subject to $C \geq \alpha_i \geq 0,$ for all $1 \leq i \leq n$ and
$$\sum_{i=1}^n \alpha_i y_i = 0$$
$w$ is recovered as $w = \sum_{i=1}^n \alpha_{i}y_{i}x_{i}$. Notice that this is similar to the linear separable case, except that there is an upper bound $C$ on $\alpha_i$ now. Once again, a QP solver can be used to find $\alpha_i$.
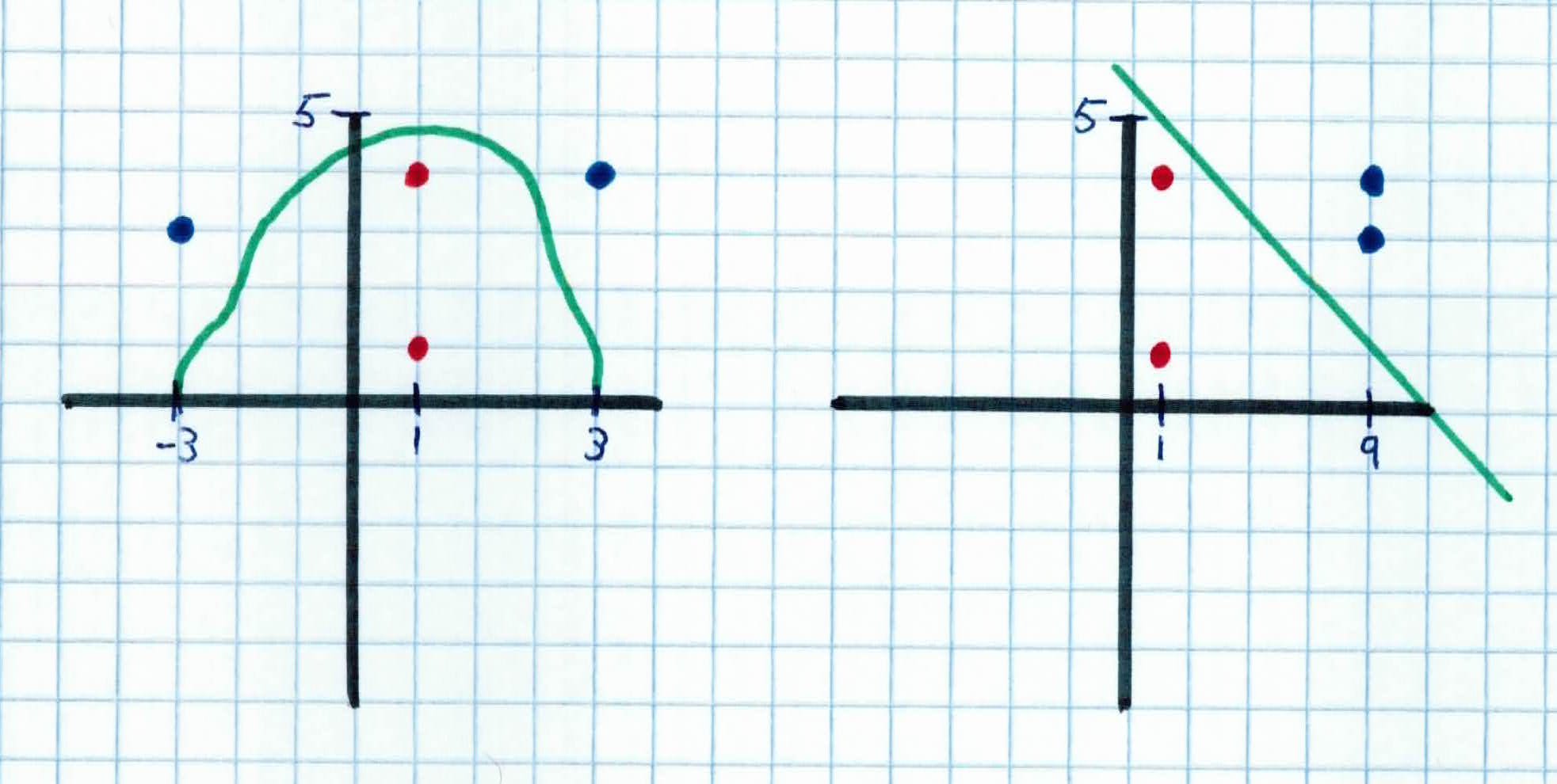
SVM also works for non-linear decision boundaries. Something that is non-linear in 2 dimensions might be linear in 3 dimensions. For example, in the figure below on the right, in 2 dimensions, there is no linear boundary to separate the examples. However, if we project those same features to 3 dimensions, we can find a linear separating hyperplane. So it would be linear in 3 dimensions and non-linear in 2.
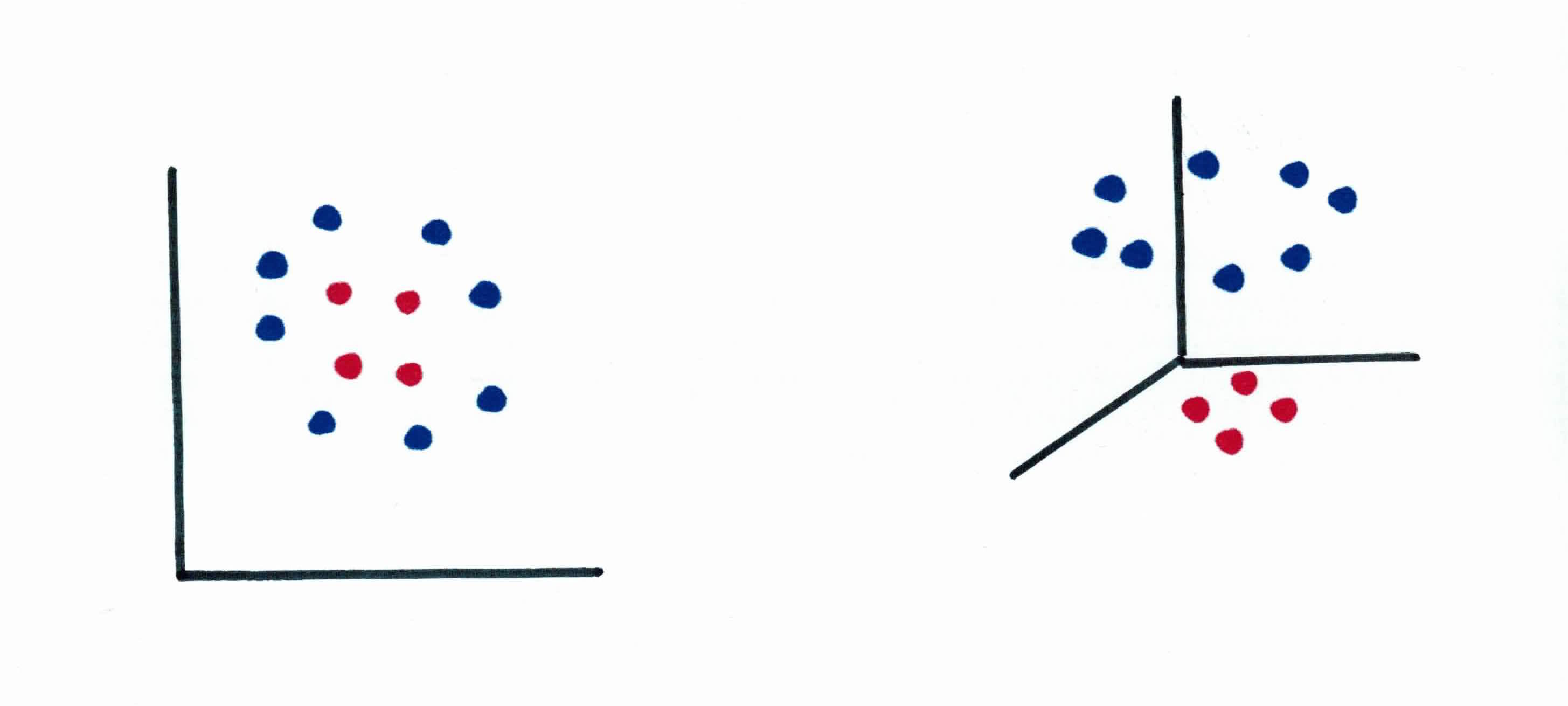
Notice above that the two data sets are the same, one is just projected to a different dimension. Another example would be one below. We use our feature mapping function $\phi(x)=(x_1^2, x_2)$ to project the data to a different dimension. For example, from below, at $x_4 = (x_{4,1},x_{4,2})= (3,4)$ once it gets put through our feature mapping function, we get $\phi(3,4) = (3^2, 4) = (9, 4)$ which corresponds to the blue point on the right. As you can see, with our feature mapping, we are able to find a linear boundary in $\phi(x)$ which corresponds to a non-linear boundary in $x$. Our new function becomes $f(x) = w^T\phi(x)+b$
Just to recap, the key idea is to transform $x$ to a higher dimensional space to make life easier. You go from the input space: the space the points $x_i$ are located and map it to the feature space, the space of $\phi(x_i)$ after transformation. You transform because linear operations in the features space is equivalent to non-linear operation in the input space. Also, classification can become easier with proper transformation. For example, in the XOR problem, adding a new feature of $x_1 x_2$ makes the problem linearly separable.
However, computation in the feature space can be costly because it is high dimensional as the feature space is typically infinite-dimensional. What can we do about this? We use the kernel trick! Recall that in our new SVM optimization problem, the data points only appear as inner product $x_i^Tx_j$. As long as we can calculate the inner product in the feature space, we do not need the mapping explicitly.
We define the kernel function K by
$$K(x_i, x_j)= \phi(x_i)^T\phi(x_j)$$
Suppose our feature mapping $\phi$ is given as follows:
$$\phi(x_i) =\phi(\left( \begin{array}{c} x_{i,1} \ x_{i,2} \end{array} \right)) = (1, \sqrt{2}x_{i,1}, \sqrt{2}x_{i,2}, x_{i,1}^2, x_{i,2}^2, \sqrt{2}x_{i,1}x_{i,2})$$
An inner product in the feature space is given by:
$$\phi(\left( \begin{array}{c} x_{i,1} \ x_{i,2} \end{array} \right))^T\phi(\left( \begin{array}{c} y_{i,1} \ y_{i,2} \end{array} \right)) = (1 + x_{i,1}y_{i,1} + x_{i,2}y_{i,2})^2$$
So, if we define the kernel function as follows, there is no need to carry out the feature mapping $\phi$ explicitly:
$$K(x,y) = (1+x_1y_1+x_2y_2)^2$$
The use of kernel function to avoid carrying out $\phi$ is known as the kernel trick.
Kernelling can be a confusing concept to understand, so I will illustrate one more example.
Say we are in 3-dimensional space and want to project to 9-dimensional space to classify the new data. The two data points we have are:
$$x = (x_1, x_2, x_3) = (1,2,3)$$
$$y = (y_1, y_2, y_3) = (4,5,6)$$
and our feature mapping $\phi(x)$ to get to 9 dimensions is
$$\phi(x) = (x_1x_1, x_1x_2, x_1x_3, x_2x_1, x_2x_2, x_2x_3, x_3x_1, x_3x_2, x_3x_3)$$
So in order to calculate the inner product in the feature space $\phi(x)^T\phi(y)$ without kernelling, we must first calculate $\phi(x)$ and $\phi(y)$
$$\phi(x)=(1,2,3,2,4,6,3,6,9)$$
$$\phi(y)=(16, 20,24,20,25,36,24,30,36)$$
We then calculate $\phi(x)^T\phi(y)$:
$$\phi(x)^T\phi(y) = 16+40+72+40+100+180+72+180+324 = 1024$$
The issue with this is, there were a lot of computational steps because of the mapping from 3 dimensions to 9. As we get to higher dimensions, the runtime increases causing some programs to crash.
Instead, we can just use the kernelling function $K(x,y) = (x^T y)^2$:
$$K(x,y) = (x^Ty)^2 = (4+ 10+ 18)^2 = 1024$$
which gives you the same result without going to higher dimensions, saving tons of computation!
Kernelling can be quite confusing. Make sure you walk through the math to see why the kernel trick saves us a bunch of computation.
Now, how exactly do we come up with kernelling functions that happen to produce the same output as the the dot product in the feature space? Unfortunately, there is no systematic way for that. It's an art and takes practice.
Another view is that the kernel function, being an inner product, is really a similarity measure between the objects. So, we simply change all the inner products to kernel functions. For training, we get
$$max W(\alpha) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n \alpha_i \alpha_j y_i y_j K(x_i,x_j)$$
$$subject \ to \ C \geq \alpha_i \geq 0, \sum_{i=1}^n \alpha_i y_i = 0$$
After finding the $\alpha's$, we can find the $w$'s with:
$$w^* = \sum_{i=1}^n \alpha_i^* y_i \phi(x_i)$$
To classify a new piece of data $z$, we have:
$$f(z) = \langle w, \phi (z) \rangle + b = sign(\sum_{i=1}^n \alpha_i^* y_i K(x_i, z) + b^*)$$
Some observations:
Given a training set ${(x_1, y_1), \ldots (x_n, y_n)}$, the SVM algorithm works like this:
A group of your friends have been infected by an alien parasite. You have a radiation beam that could kill the parasite, but it's so strong that it could also kill your friends if its on them for too many seconds. If it's too few seconds, then the parasite will not be exterminated.

Your job is to use SVM to build a model and classify whether or not your radiation beam was successful. You have already deployed the beam on 5 of your friends. One was successfully treated, the other 4 were not. The features given are how many seconds the beam was on your friend:
$$x_1 =1, \ y_1 = 1 $$
$$x_1 =2, \ y_2 = 1 $$
$$x_1 =3, \ y_3 = -1 $$
$$x_1 =4, \ y_4 = 1 $$
$$x_1 =5, \ y_5 = 1 $$
As you can see, thus far, your only friend that survived is the one that had the radiation beam on him for 3 seconds (survived=-1).
$C$ is set to 1000 and we use the polynomial kernel of degree 2, given by:
$$K(x,y) = (xy+1)^2$$
We first find $\alpha_i$ for all $1 \leq i \leq 5$:
$$max\sum_{i=1}^5 \alpha_i - \frac{1}{2}\sum_{i=1}^5 \sum_{j=1}^5 \alpha_i \alpha_j y_i y_j (x_i x_j +1)^2$$
$$subject \ to \ 1000 \geq \alpha_i \geq 0 \ and \ \sum_{i=1}^5 \alpha_i y_i = 0$$
By using a QP solver, we get:
$$\alpha_1 = 0, \alpha_2 = 21.99, \alpha_3=37.98, \alpha_4 = 15.99, \alpha_5 = 0$$
Note that the constraints are indeed satisfied.
Recall, that support vectors correspond to the non-zero $\alpha's$, so the support vectors are ${x_2 = 2, x_3 = 3, x_4 = 4 }$
The discriminant function we get from above is:
$$f(z) = 21.99(1)(2z+1)^2 + 37.98(-1)(3z+1)^2 + 15.99(1)(4z+1)^2 + b$$
$$=1.98z^2 - 12z + b$$
$b$ is then recovered by solving $f(2) = 1$, $f(3) = -1$, or $f(4) = 1$, as $x_2$ and $x_4$ lie on the line $\phi(w)^T\phi(x) + b =1$ and $x_3$ lies on the line $\phi(w)^T \phi(x) + b = -1$
All three give $b = 17.08$ so our discriminant function is now:
$$f(z) = 1.98z^2 - 12z + 17.08$$
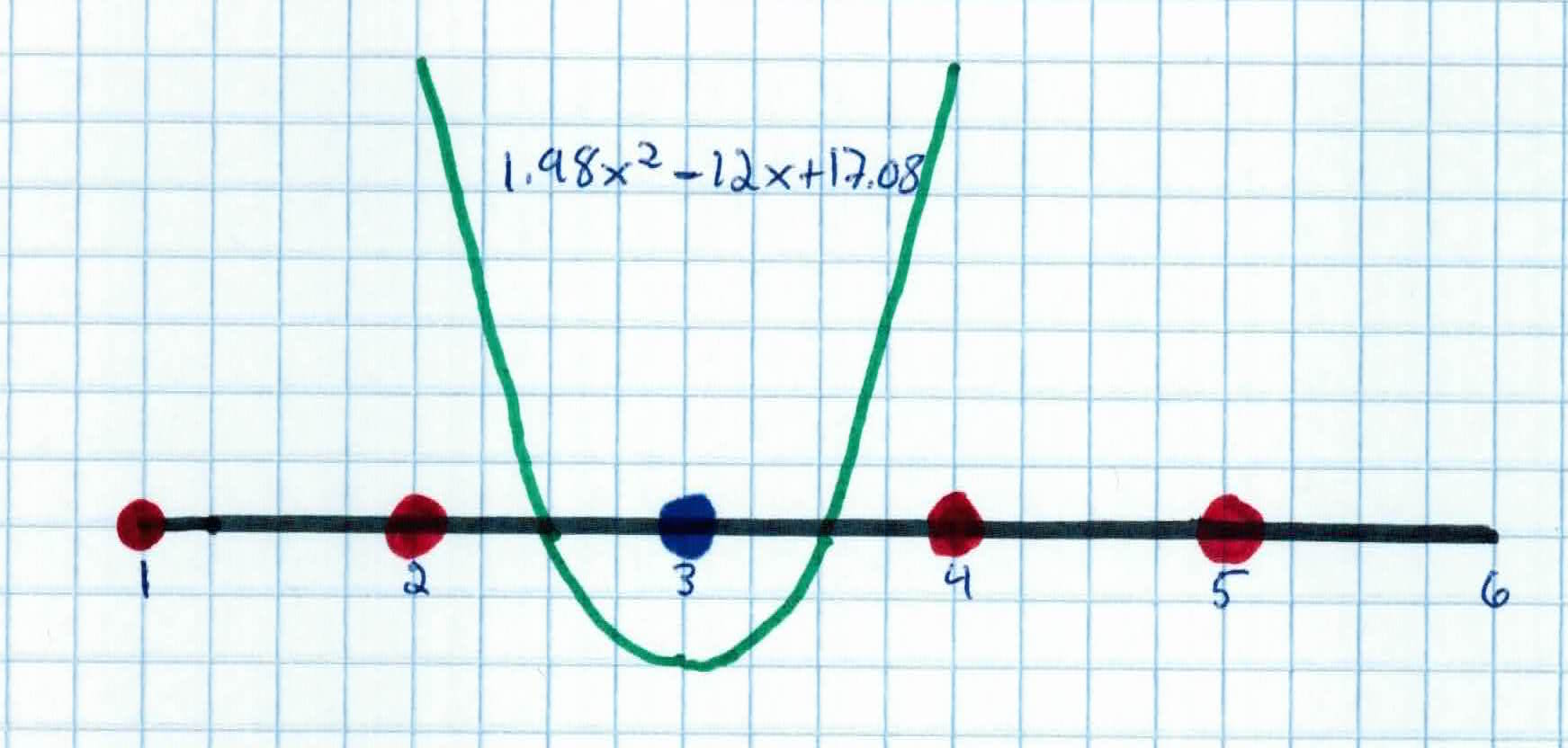
So, for our 6th friend $x_6$ -- who's been under the radiation for 3.3 seconds -- we want to see if his treatment was successful.
We simply plug him into our discriminant function:
$$(z) = sign(1.98z^2 - 12z + 17.08)$$
$$f(3.3) = sign(1.98(3.3)^2 - 12(3.3) + 17.08)$$
$$= sign(1.98(10.89) - 39.6 + 17.08)$$
$$= sign(-.9578) = -1$$
By our model, we see that 3.3 seconds was enough time for the radiation beam to remove the parasite but not long enough to harm our friend. He is classified as safe!
Support Vector Machines are a powerful supervised learning method that build on the intuition that a hyperplane that maximizes the margin between classes provides the most optimal model. The purpose of SVM is to train a model to assign new, unseen data into a certain class. It achieves this by creating a linear partition of the feature space into two classes. Based on the features of the new data, it places it on once side of the linear separator, leading to a categorization.
We have discussed and formalized what we mean by margin and introduced the primal problem to maximize the margin. We then took a digression to discuss Langragian multipliers so that we could introduce the dual problem, a problem that would bring the same solution, but easier to compute. We then extended the problem to non-linearly separable data by introducing soft margin classification with slack variables. We finally introduced kernels which would allow us to implicilty project the data to higher dimensions to find non-linear decision boundaries in the original dimension.
Other observations: