
Linear regression is the most basic type of regression and commonly used in predictive analysis. Unlike the previous algorithms, linear regression can only be used for regression as it returns a real predicted value, i.e. 567 dollars per share, or predicting your son grows to be 6ft4. It models the relationship between dependent variable $y$ and one or more independent variables $x$ by fitting a linear equation to observed data. Linear regression finds the linear trend within the data with weights (parameters), and uses that to predict real values. We use gradient descent or normal equations to find the proper weights.
You're going to Europe to study abroad and the only option for your living situation is this house in the middle of nowhere, 45 mins away from university. The weather in the area is mysterious, as it's raining 24/7. It's an old, wooden house and has a melancholic vibe to it. It seems abandoned, maybe even haunted.

You get settled in and decide to take a more detailed tour of the house. You walk into the basement and you see a bloody knife stabbed into the wall. You think nothing of it.
You go about your day. The next morning, you go to the basement to wash some clothes. You're putting your clothes in the dryer and you notice a second knife stabbed into the wall. You think maybe you just didn't catch it yesterday.
By day four, you see four knives, and you begin to realize that the house just might be haunted. You pack up your bags and attempt to leave but all the doors are locked shut and there is no service to make a phone call. You go back into your room and hope it was all just a dream. Days go by and the new knifes continue stacking up.
Finally, after 10 days you hear a voice. The voice tells you that you if you can predict where the next knife will go, it will open the doors and let you free. Else, you are stuck in the house for eternity.
You go to the basement and you see 10 knives stabbed into the wall. Your jobs is to predict where the 11th knife will go.
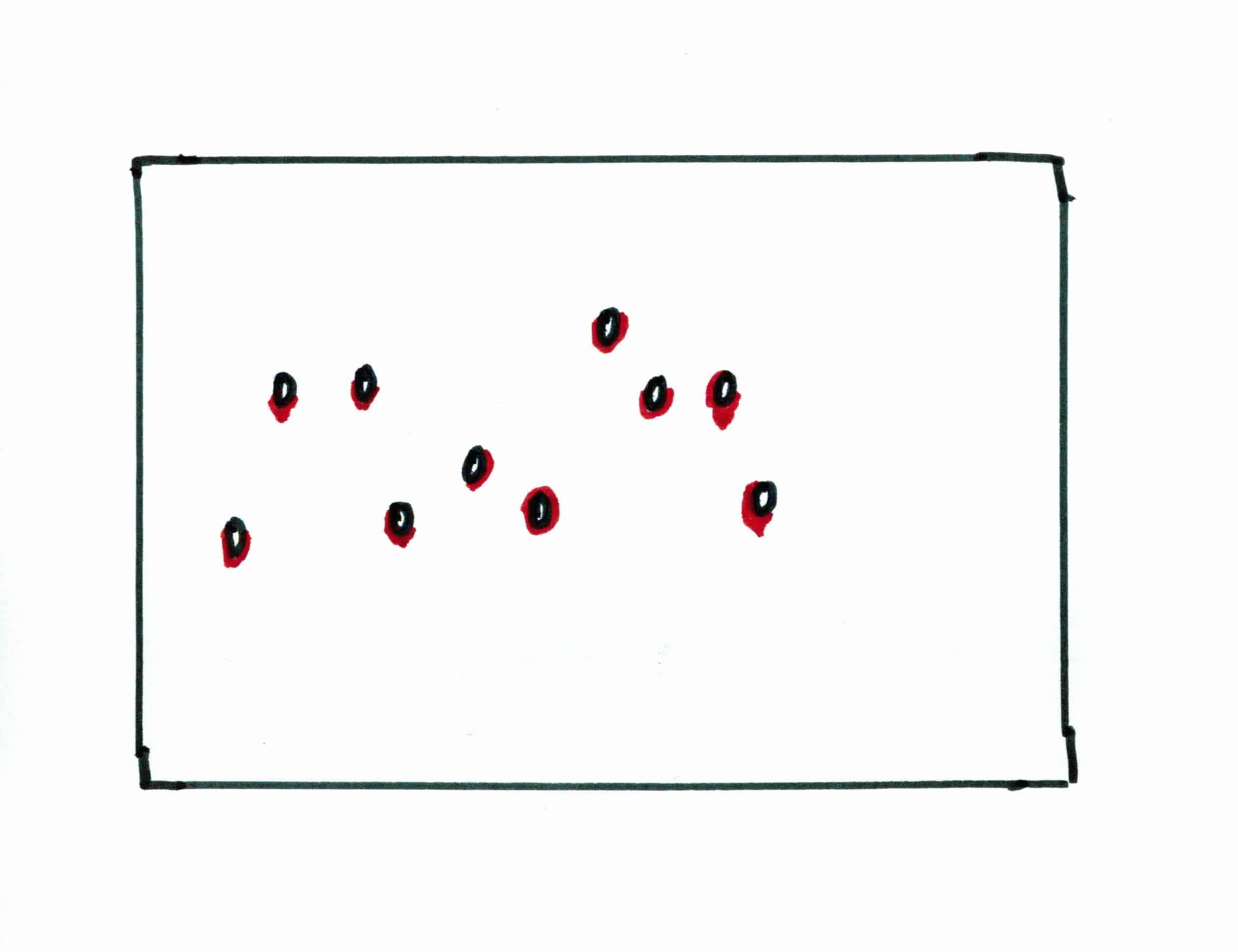
You notice that there is a linear pattern in how the knives are being placed. Being the logical person you are, you realize your best bet is to approximate the pattern with a straight metal rod. How do you know where to place the rod to approximate the linear pattern the best? You use rubber bands.
You have 10 rubber bands, all of the same (small) size, and unbreakable. You tie each rubber band onto a knife and tie the rubber band to the metal rod directly above/below the respective knife, fully stretching each one.
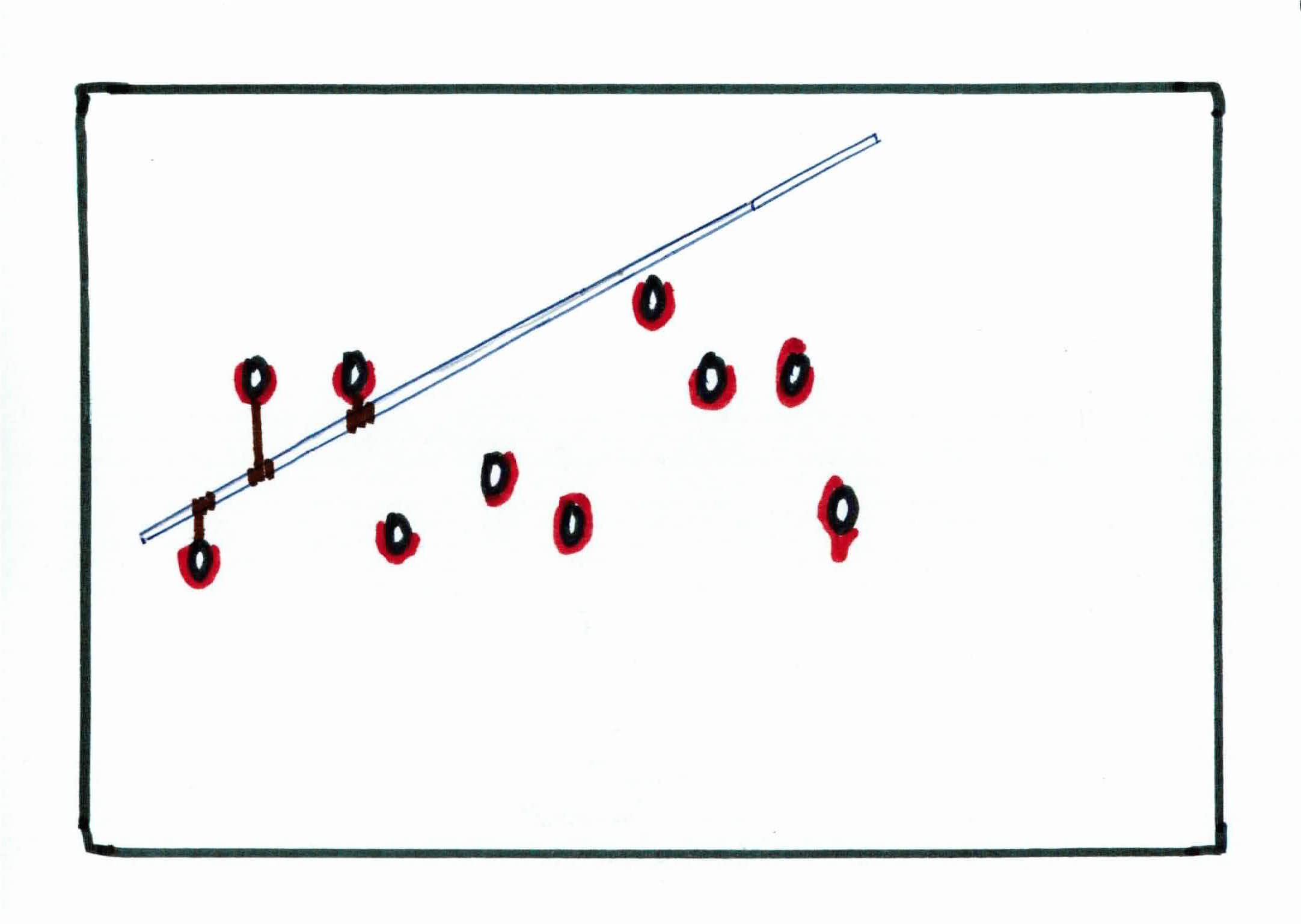
Your goal is to find the best line (metal road) to approximate the data (knives). We can achieve that by minimizing the total vertical distance from the knives to the metal road. This is done naturally with the rubber bands, as the elastic energy of each rubber band will try to minimize the stretching as best as it can. Once it has reached equilibrium (convergence), you will see that the metal rod has done a pretty good job of approximating the pattern.
You then use the metal rod to predict where you thing the next knife will be placed. This is your best bet. You draw a red mark at that spot and go to sleep.
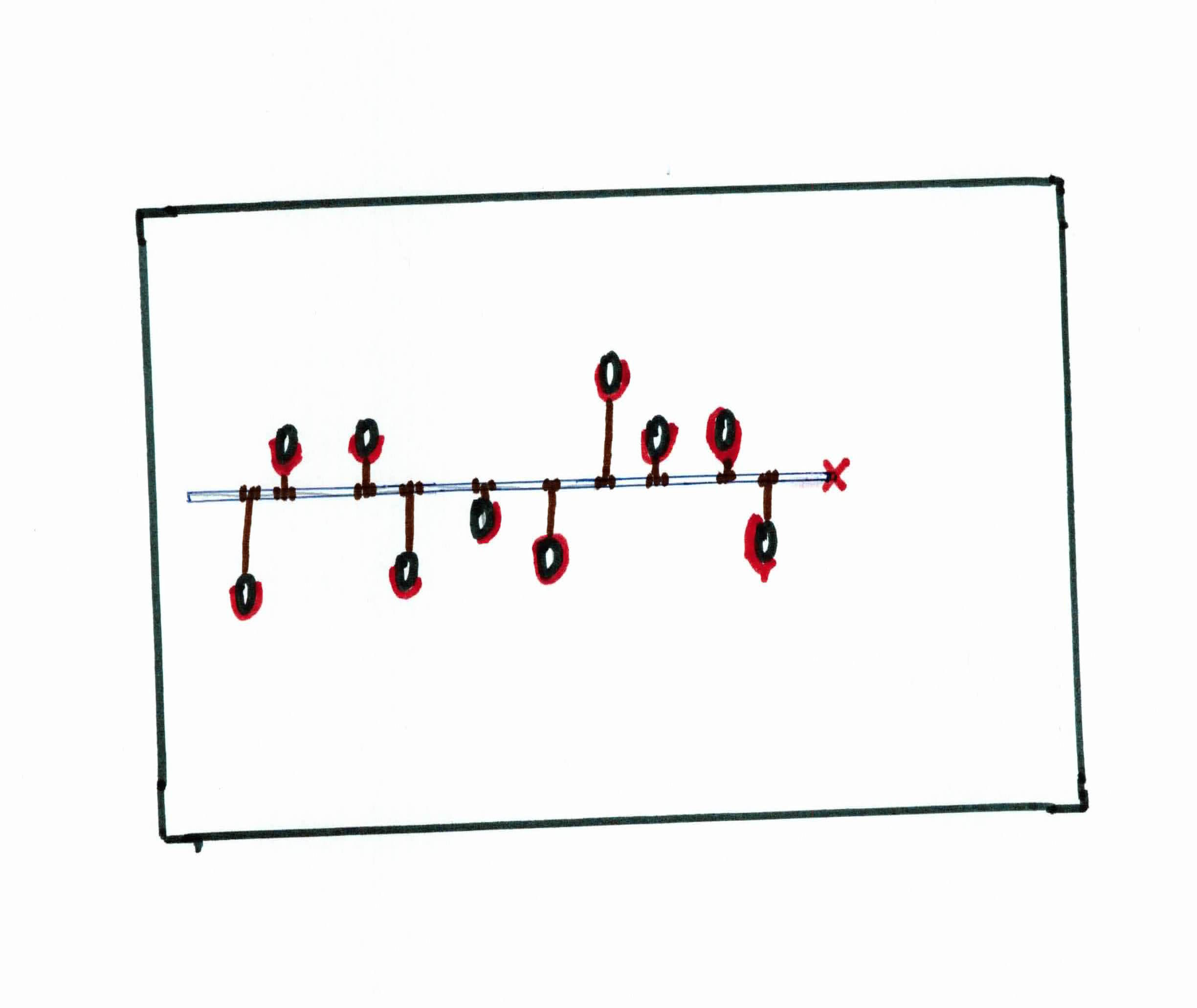
The next day, you see the sky has cleared up, the sun is out, and all the doors are unlocked. You have predicted the 11th knife correctly and are now set free.
Linear regression attempts to fit a line to the data where the target value is expected to be a linear combination of the input variables. It fits a linear model with coefficients/weights $w=(w_1, \ldots, w_n)$ to minimize the residual sum of squares between the observed responses in the dataset and the responses predicted by our linear approximation.
So, in 3 dimensions, this means we are trying to minimize the total distance between the plane and all of those points (residual sum of squares). This results in a linear plane that approximates our data.
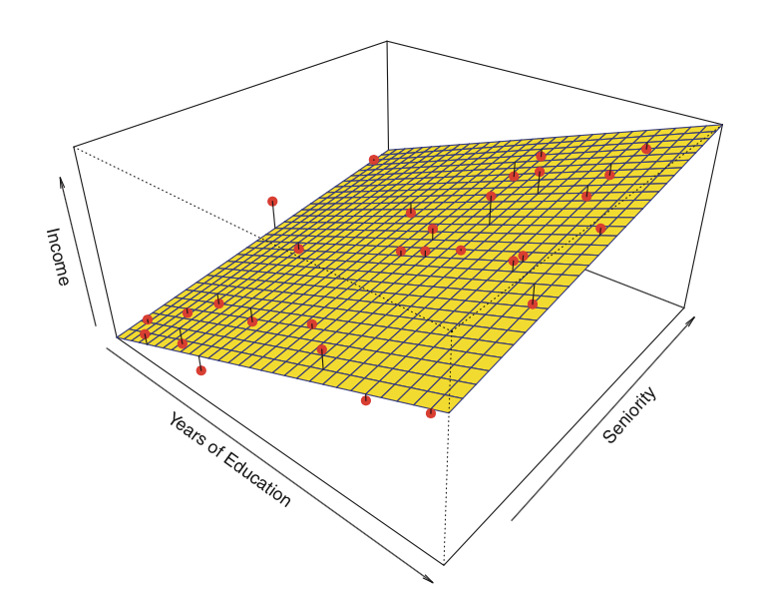
Given training data $(x_1, y_1), \dots, (x_n,y_n)$ with $d$ features, where $x_i \in \mathbb{R}^d$ and $y_i \in \mathbb{R}$ we want to learn a regression function $f : \mathbb{R}^d \rightarrow \mathbb{R}$ so that it returns a real value instead of a class.
Regression model is said to be linear if it is represented by a linear function. Our linear regression model is given as:
$$f(x) = w_0 + \sum_{j=1}^d w_j x_j$$
with $w_j \in \mathbb{R}$ for all $1 \leq j \leq d$
$w$'s are called parameters or coefficients or weights. So, learning the linear model means learning the $w$'s of the model. But how do we learn the $w$'s and how do we check how well your model ($w's$) is performing? We use least square loss:
$$loss(y_i, f(x_i)) = (y_i - f(x_i))^2$$
Notice that this is the difference between our predicted answer and the actual answer. We should want to reduce this difference for an accurate model.
We want to minimize the loss over all examples, that is minimize the residual sum of squares we talked about. We call this our cost function $J$:
$$J = \frac{1}{2n}\sum_{i=1}^n(y_i - f(x_i))^2$$
Our goal is to find the weights $w$ that minimize the above cost function.
For example, imagine we just had one feature $(d=1)$:
$$f(x)= w_0 + w_1 x$$
Notice that this is the same as the equation for a line $b+mx$.
We want to minimize:
$$J = \frac{1}{2n} \sum_{i=1}^n(y_i - f(x_i))^2$$
$$J(w) = \frac{1}{2n} \sum_{i=1}^n(y_i - w_0 - w_1 x_i)^2$$
We want to find $w_0$ and $w_1$ that minimizes the above function. So, we're left with:
$$ argmin_{w} \frac{1}{2n} \sum_{i=1}^n(y_i - w_0 - w_1 x_i)^2$$
With more than one feature, we could write it as:
$$J(w) =\frac{1}{2n} \sum_{i=1}^n (y_i - w_0 - \sum_{j=1}^d w_j x_{ij})^2$$
to find the $w$ that minimizes $J(w)$
When you have the $w$'s, that is your model. You formed those $w$ from your training model. When you have new data, you can then multiply it with those $w$ and get a (hopefully) accurately predicted label.
Remember, finding the weights that minimize the cost function means that you found the weights that form the best line/plane to approximate your data.
You can look for those $w$ by using 1 of 2 methods: gradient descent or normal equations. Both have their pros and cons. We will go over gradient descent first.
Before discussing gradient descent, make sure you are familiar with partial derivatives/gradients.
Remember that our goal is to find the $w$'s that make $f(x)$ close to $y$, which is the same as minimizing the cost function $J(w)$. If we plot our cost function as a function of $w$, we get:
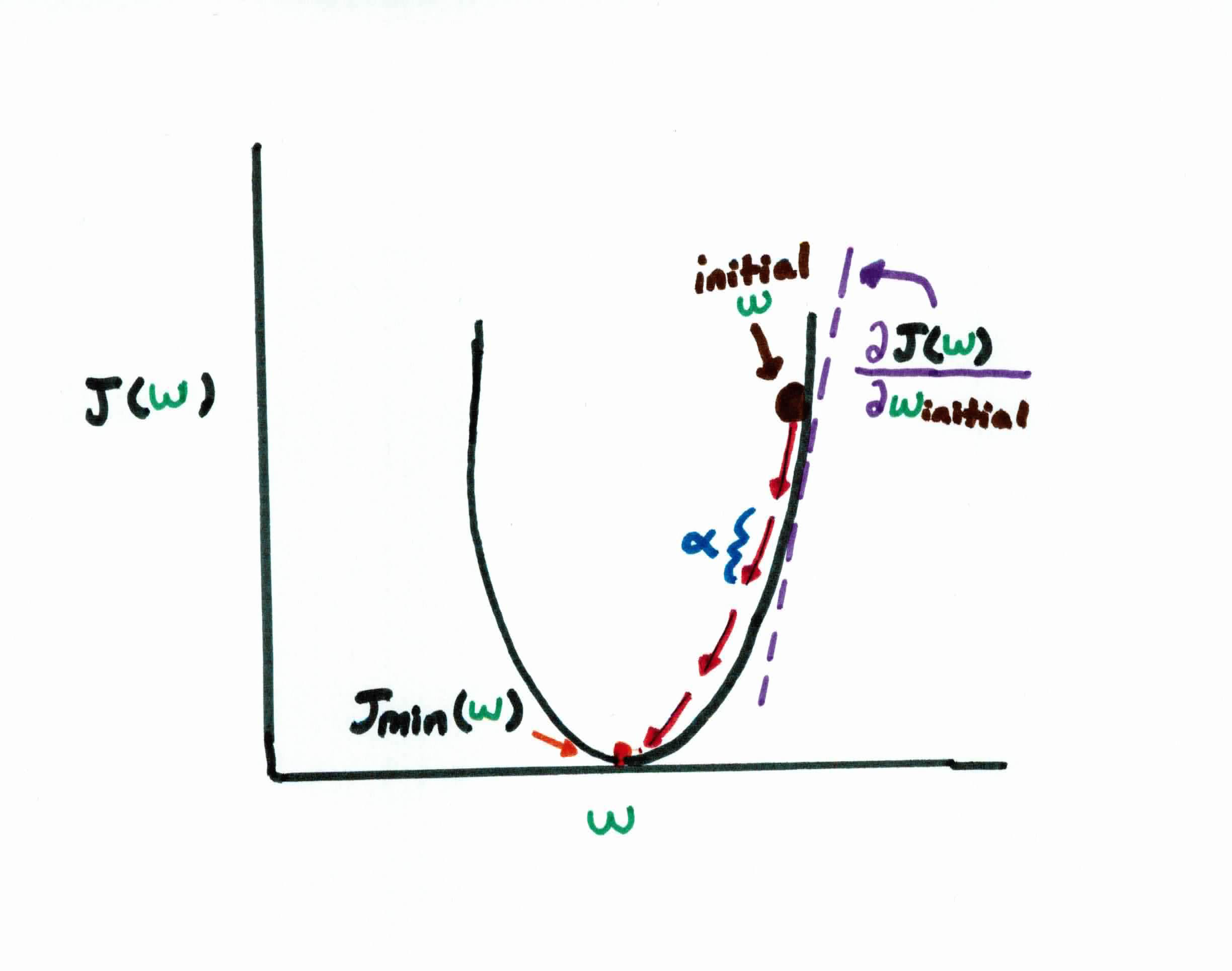
As you can see, our error curve is convex, meaning we can simply find the minimum cost by finding the $w$'s that result in the bottom of the graph, known as the global minima.
To do so, we use gradient descent to start with some initial guess for $w$, and we repeatedly change it to make $J(w)$ smaller. Think of it as, you are weight $w_j$ and you take a step of size $\alpha$ in the opposite direction of $\frac{\partial}{\partial w_j} J(w)$. You repeatedly move in this direction until you find this minimum.
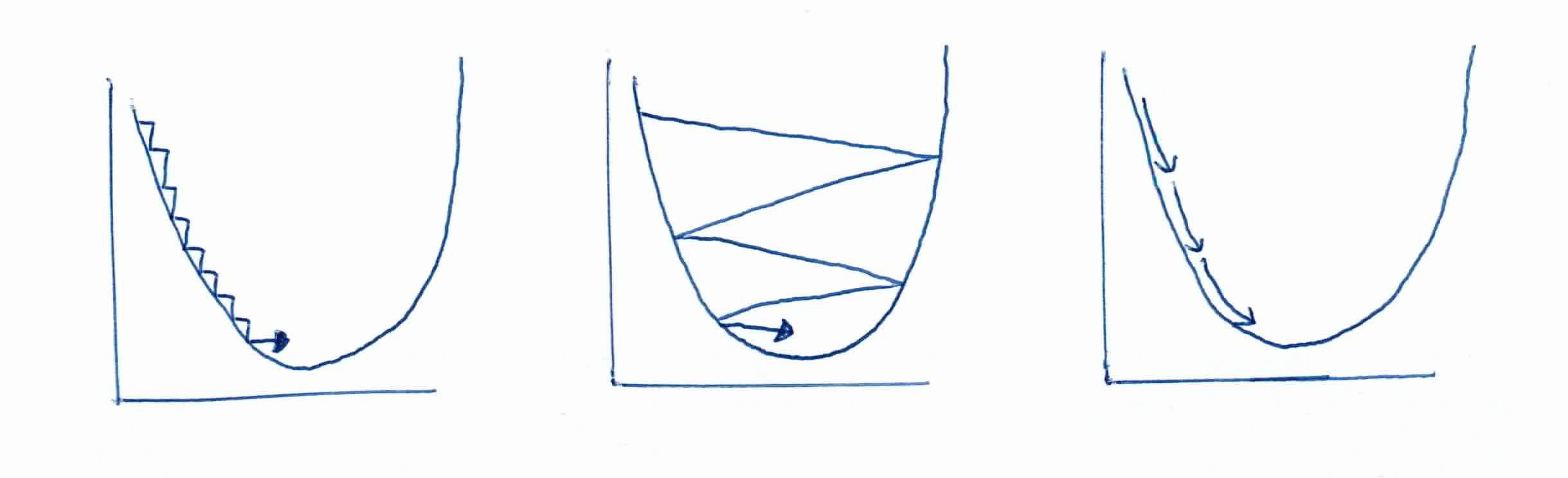
Choosing the right step size $\alpha$ is extremely important. You want to get to the center, so naturally you'll go the opposite direction of $\frac{\partial}{\partial w_j} J(w)$(partial derivative/slope), but the actual step size is determined by $\alpha$. If the step size is too small, it will take an extremely long time to converge. If it's too large, you'll overshoot the global minimum. You must find just the right $\alpha$.
Recall that you can find the minimum by finding where the derivative is zero. So minimize $J(w_0, w_1)$, that is:
$$\frac{\partial J}{\partial w_0}=0$$
$$\frac{\partial J}{\partial w_1}=0$$
$$\frac{\partial J}{\partial w_0}=2 \times \frac{1}{2n} \sum_{i=1}^n (y_i - w_0 - w_1 x_i) \times \frac{\partial}{\partial w_0}(y_i - w_0 - w_1 x_i)$$
$$\frac{\partial J}{\partial w_0} = \frac{1}{n}\sum_{i=1}^n (y_i - w_0 - w_1 x_i) \times (-1) = 0$$
and for $w_1$:
$$\frac{\partial J}{\partial w_1}=2 \times \frac{1}{2n} \sum_{i=1}^n (y_i - w_0 - w_1 x_i) \times \frac{\partial}{\partial w_1}(y_i - w_0 - w_1 x_i)$$
$$\frac{\partial J}{\partial w_1} = \frac{1}{n}\sum_{i=1}^n (y_i - w_0 - w_1 x_i) \times (-x_i) = 0$$
We can then update -- simultaneously -- all $w_j$ for $(j=0$ and $j=1)$ to slowly converge to that minimum point:
$$w_0 := w_0 - \alpha \frac{\partial}{\partial w_0}J(w_0, w_1)$$
$$w_0 :=w_0 -\alpha \frac{1}{n} \sum_{i=1}^n (w_0 + w_1 x_i - y_i)$$
$$w_1 := w_1 - \alpha \frac{\partial}{\partial w_1}J(w_0, w_1)$$
$$w_1 :=w_1 -\alpha \frac{1}{n} \sum_{i=1}^n (w_0 + w_1 x_i - y_i)(x_i)$$
We repeat this step until our gradient is near zero, which is where we find our minimum. We call this convergence. This is known as an iterative method because we slowly update the $w$ until we reach a minimum point.
The second way is to solve it analytically in a closed-form with normal equations
Let's first try to write everything elegantly with matrices.
Let $X$ be a $n \times (d+1)$ matrix where each row starts with a 1 followed by a feature vector.
Let $y$ be the label vector of the training set.
Let $w$ be the vector of weights (that we want to estimate).
$$ X :=\left( \begin{array}{ccccccc} 1 & x_{11} & \dots & x_{1j} & \dots & x_{1d} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & x_{n1} & \dots & x_{nj} & \dots& x_{nd} \end{array} \right)$$
$$y := \left(\begin{array}{c} y_1 & \vdots & y_i & \vdots & y_n \end{array} \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ w := \left(\begin{array}{c} w_0 & \vdots & w_i & \vdots & w_n \end{array} \right)$$
Recall that we appended 1's to the $X$ matrix first column because when we multiply it with the weight vector, for any $x_i$ we get $w_0(1) + \sum_{j=1}^d w_j x_{ij}$ which is what we needed.
We want to find $(d+1) \ w$'s that minimize J. We have:
$$J(w) = \frac{1}{2n} \Vert (y-X w) \Vert ^2$$
$$J(w) = \frac{1}{2n}(y-X w)^T(y-X w)$$
$$\frac{\partial J}{\partial w}=-\frac{1}{n}X^T(y-X w)$$
Remember, in order to find the minimum, we must set $\frac{\partial J}{\partial w}$ to zero, so:
$$X^T(y-Xw)=0$$
Moving a few pieces around, we see that the unique solution is then:
$$w = (X^TX)^{-1}X^Ty$$
Notice that if we take the second partial derivative, we have that:
$$\frac{\partial^2J}{\partial w}=-\frac{1}{n}X^TX$$
is positive definite which ensures that that $w$ is a minimum.
I can't stress this enough. The purpose of these algorithms is to find the optimal weights that form a line/plane that best approximates your data. This line/plane can then be used to predict new information
Given a training set ${(x_1, y_1), \ldots (x_n, y_n)}$, with all training examples in matrix $X$, and all training labels in vector $y$, the algorithm (Normal Equations) to find the weights for Linear Regression works like this:
You're a real estate agent trying to predict your career trajectory. So far, you've been in the game for 6 years and have sold 4 homes. At year 1, you sold 2 homes. By year 3, you have sold 3 homes. This year (year 6), you have sold 4 homes. This is your training data:
$$x_1 = 1, y_1 = 2$$
$$x_2 = 3, y_2 = 3$$
$$x_3 = 6, y_3 = 4$$
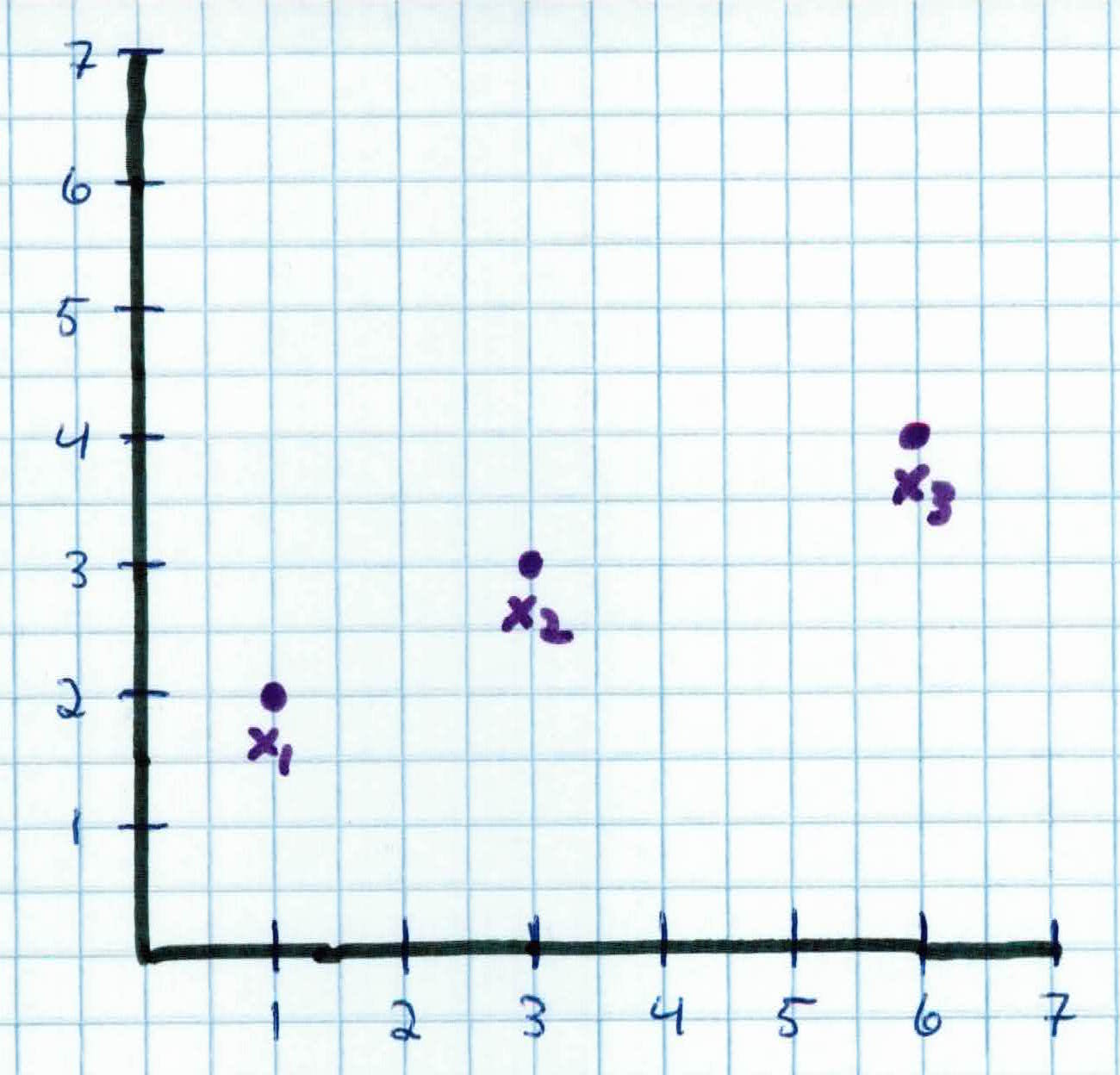
You want to predict how many homes you would have sold 12 years from now, at year 18. We could solve it by gradient descent, but instead of iterating, we could just use normal equations to solve it analytically.
We first append a 1 to each training example, which would act as the bias $w_0$, giving us:
$$X = \left(\begin{array}{cc} 1 & 1 \\ 1 & 3 \\ 1 & 6 \end{array} \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Y = \left(\begin{array}{c} 2 \\ 3 \\ 4 \end{array} \right)$$
We use matrix multiplication to calculate:
$$X^TX = \left(\begin{array}{ccc} 1 & 1 & 1 \\ 1 & 3 & 6 \end{array} \right) \left(\begin{array}{cc} 1 & 1 \\ 1 & 3 \\ 1 & 6 \end{array} \right) =\left(\begin{array}{cc} 3 & 10 \\ 10 & 46 \end{array} \right)$$
We then take it's inverse:
$$ (X^TX)^{-1} =\left(\begin{array}{cc} \frac{23}{19} & -\frac{5}{19} \\ -\frac{5}{19} & \frac{3}{38} \end{array} \right)$$
Use matrix-vector multiplication:
$$X^TY = \left(\begin{array}{ccc} 1 & 1 & 1 \\ 1 & 3 & 6 \end{array} \right) \left(\begin{array}{c} 2 \\ 3 \\ 4 \end{array} \right) = \left(\begin{array}{c} 9 \\ 35 \end{array} \right) $$
Solving for our weights $w$, we get:
$$w = (X^TX)^{-1}X^TY = \left(\begin{array}{c} 1.68 \\ .394 \end{array}\right)$$
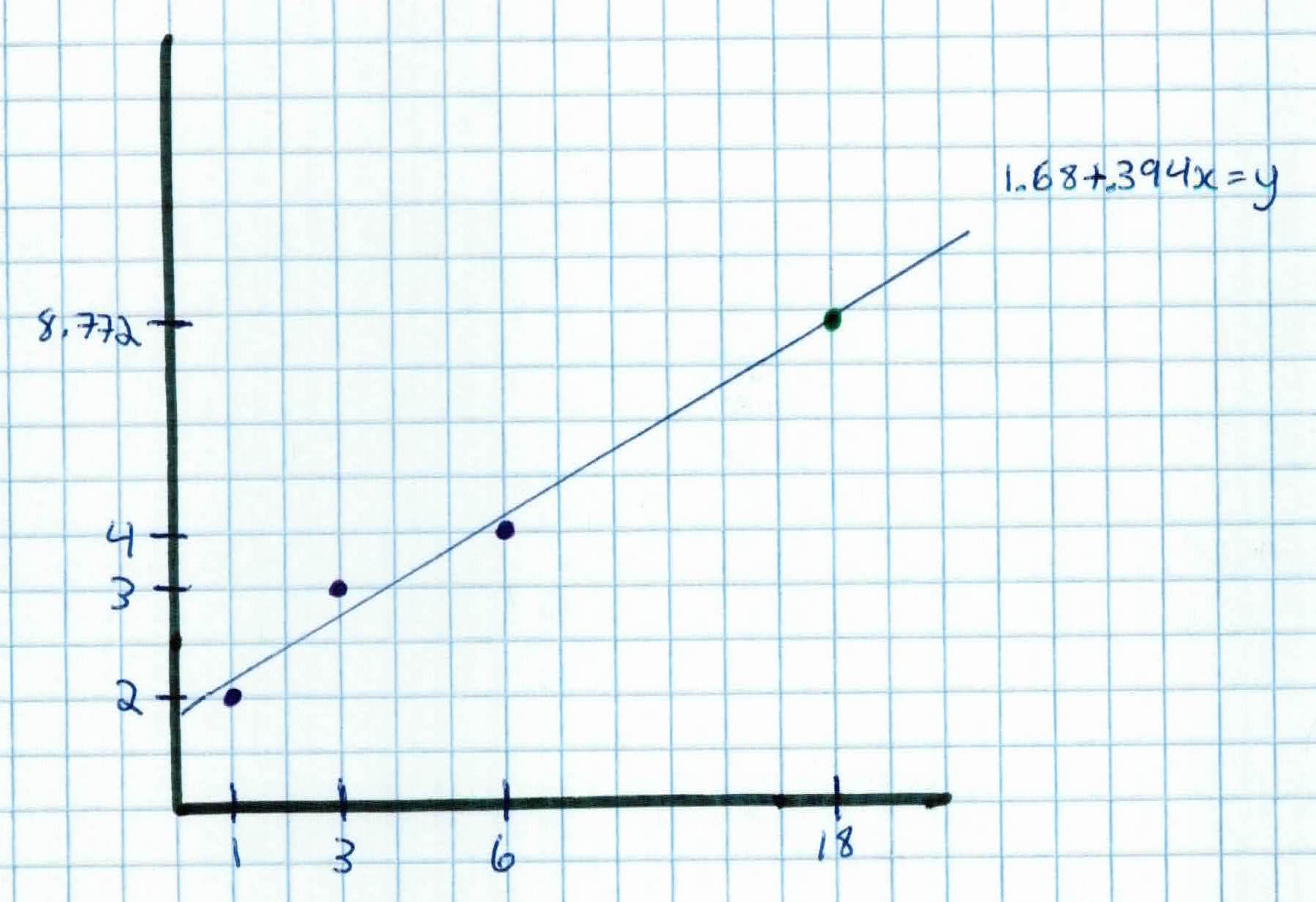
So, to predict for $X_{new} = 18 $, which is how many homes we will sell by year 18, we first append 1 for the bias:
$$X_{new} = \left(\begin{array}{cc} 1 \\ 18 \end{array}\right)$$
And we simply calculate:
$$X_{new}^T w = \left(\begin{array}{cc} 1 & 18 \end{array}\right) \left(\begin{array}{c} 1.68 \\ .394 \end{array}\right) = 8.772 $$
So, based on our algorithm and model, by year 18 we would have sold about 9 homes! Our line is given by $1.68 + .394x = y$
Linear regressions's relationships are modeled using linear predictor functions whose unknown parameters are estimated from the data. Such models are called linear models. One variable is the explanatory variable $x$, and the other is the dependent variable $y$. Like all forms of regression analysis, linear regression focuses of the conditional probability distribution $p(y\mid x)$, rather than on the joint probability distribution $p(x, y)$, which is the domain of multivariate analysis.
In order to find the right weights $w$ to fit a line to the data, we had to use gradient descent or normal equations. Once the optimal weights $w$ are found, we can then use that model to predict the value of any new data $x_{new}$.
Other observations: