$K$-Means is an unsupervised learning algorithm, meaning that you don't have the label. The purpose of the algorithm is to partition the data into $K$ ($K$ can be set to any number) different groups so you can find some unknown structure and learn what they belong to. First, you start off with $K$ clusters randomly placed. Then you assign each data point to the cluster it's closest to. You then take the average of each cluster and move each centroid (center of each cluster) to their averages. This process continues until convergence, successfully grouping the data and finding structure.
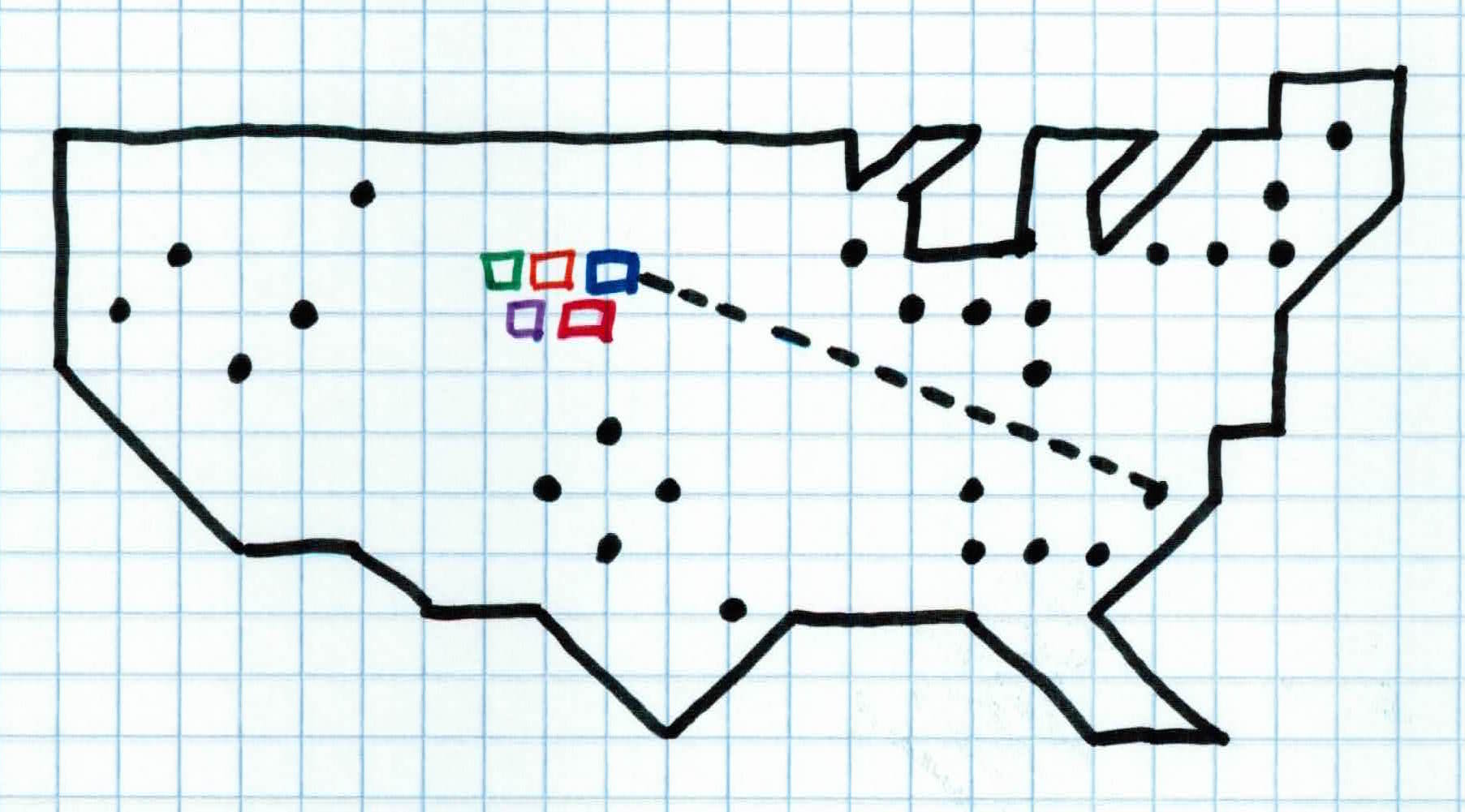
Let's say you are an evil overlord and you want to use your mind controlling device to manipulate all of America. Your device plays a loud sound and when people hear it, they become controlled by you. The further away someone is from your device, the weaker the signal. You have 5 copies of it. The most optimal way for you to control everyone is to have all 5 devices spread out across the country. If all the devices are near each other, then only a small fraction of people will be controlled by a strong signal and a majority of people around the country will be controlled by a weak signal.

So, you randomly place all 5 devices near the middle of the country (initialization step). Each device activates and everyone (data points) in the country is controlled by the device closest to them (assigning to cluster). This is not optimal because people who live on the east and west coast are controlled by a weak signal which could possibly jeopardize your evil plan. So, for each device, we find the location of where it's average signal strength is at (mean of cluster). We then relocate each device to that location (placing centroid). We then activate the devices again, having everyone controlled by the device closest to them.
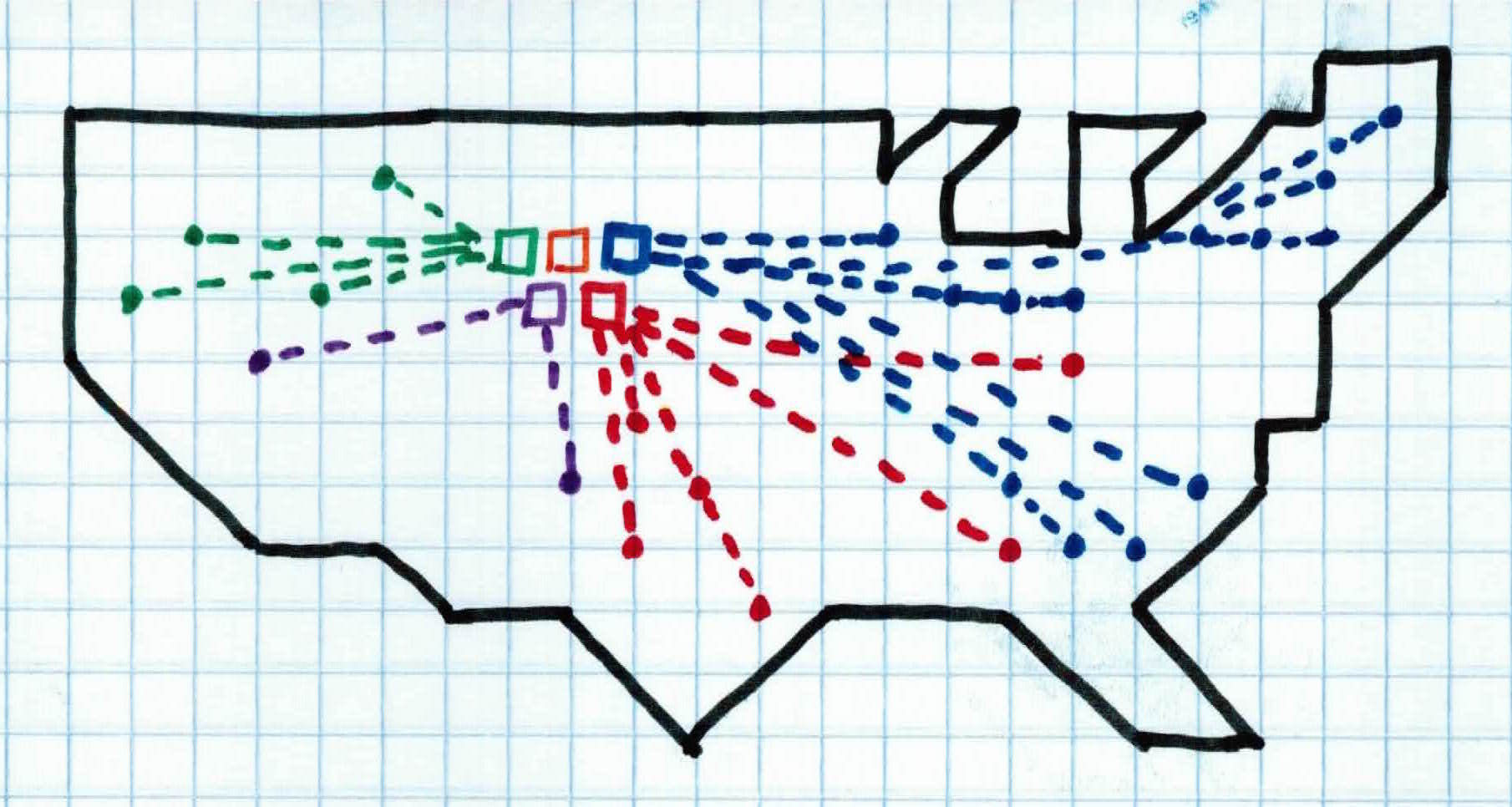
We repeat these steps until convergence. Once we reach convergence, we have the devices spread out across the people of the country, efficiently controlling all people with solid signals.
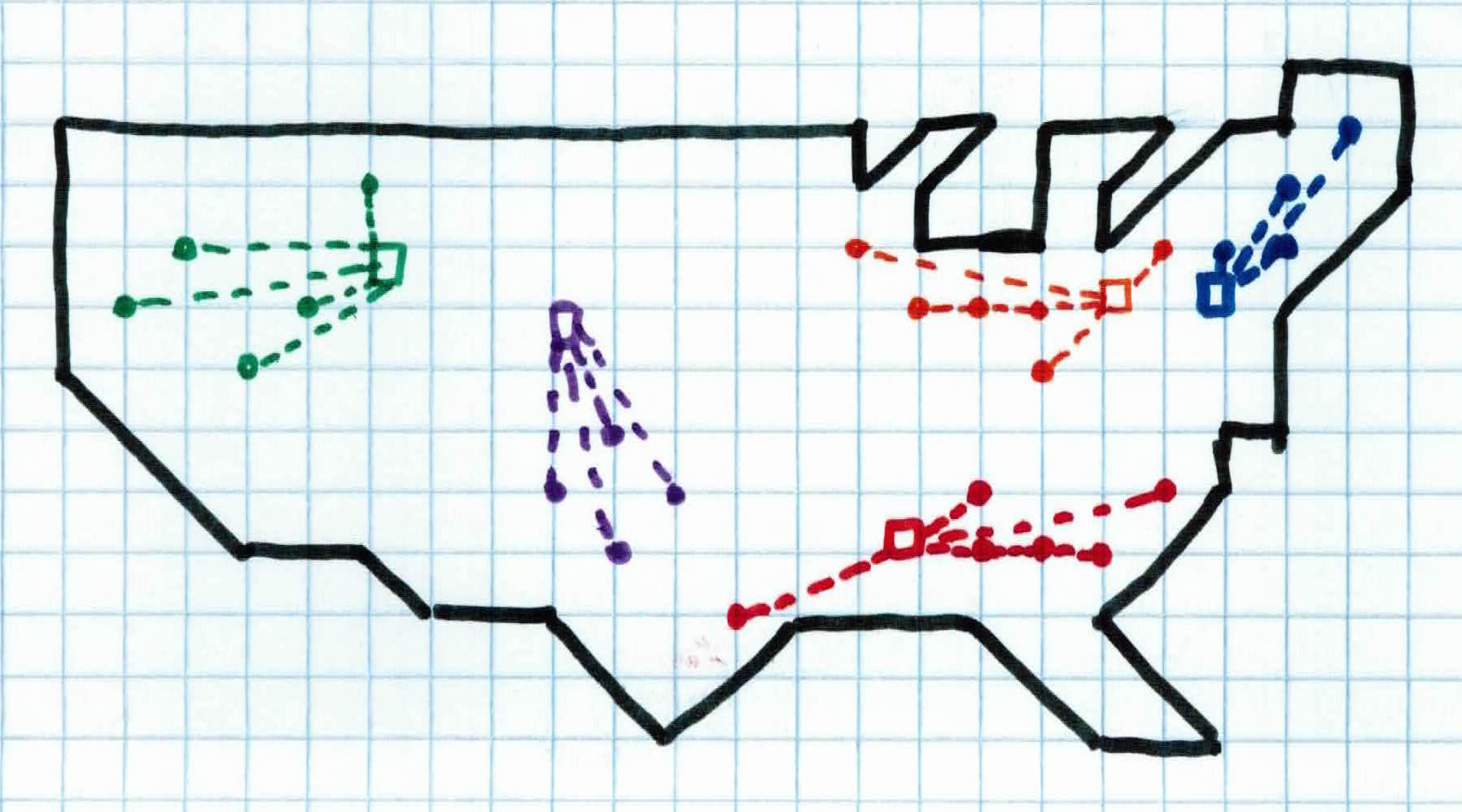
Upon further investigation, we see that the devices have also grouped specific type of people. Each device has grouped people who all have properties in common, without us looking for it. We see that the people in device green, blue, and orange are mostly affiliated with the democratic party and the people controlled by device purple and red are mostly affiliated with the republican party. We have found a way to group similar people together without knowing what to look for.
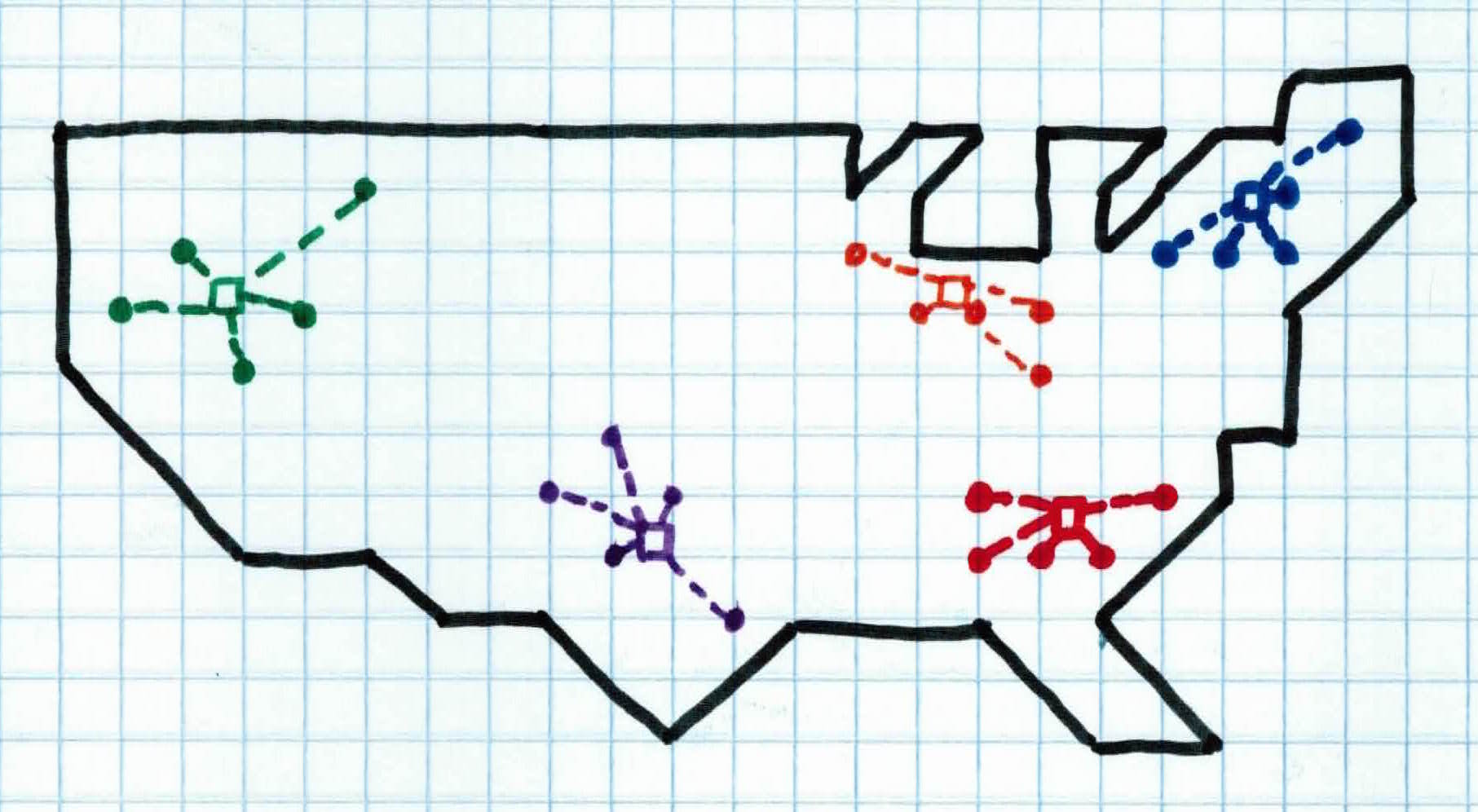
This is precisely what clustering is set out to do. Find structure, determining the intrinsic grouping in a set of unlabeled data.
Most of the algorithms I will discuss are supervised learning algorithms, meaning that they are presented with a label during the training phase. You take the data, with the label, and train your model to recognize patterns in the data that will lead to their respective labels. That way, when you have new data, your model will be able to classify/predict what label/class the new data belongs to. K-Means clustering, however, is an unsupervised algorithm, meaning there is no label in the training data. The purpose is to find hidden patterns or groupings in the data.
For example, if you had 500 dogs and knew all of their features (size, bark level, color, etc.) but had no idea what their breeds were (no label), you could simply run a clustering algorithm that would group together all the dogs with similar features. At the end of the clustering, all the dobermans, pit bulls, and corgis would be clustered into 3 different groups, even if you didn't know that's what they were called.

$K$-means clustering aims to partition $n$ observations into $K$ clusters in which each observation belongs to the cluster it's closest to. The goal after convergence is to have the data partitioned into $k$ groups that will grant us underlying information that we didn't already know.
Given training examples $x_1, \dots, x_n$ where $ x_i \in \mathbb{R}^d$ and target cardinality $k \in \mathbb{N}$, our goal is to assign each example $x_1, \dots, x_n$ to one of the *k* clusters ${C_1, \dots, C_k}$.
In order to assign each example $x_i$ to the cluster $C_k$ that its closest to, we must calculate the Euclidean distance. Given two examples $x_i$ and $x_j$, the euclidean distance between two points is given as:
$$d(x_i, x_j) = \sqrt{\sum^d_{k=1}(x_{ik}-x_{jk})^2}$$
So, first, we initialize *K *clusters randomly. We then calculate the euclidean distance between each example and each cluster:
$$d(C_t, x_i) \ for \ all \ 1 \leq t \leq k \ and \ 1 \leq i \leq n$$
We then assign each example $x_i$ to the cluster $C_k$ it is closest to.
Once we have all examples assigned to the closest cluster, we then calculate the mean of each cluster:
$$\mu_j = \frac{1}{\mid C_j\mid}\sum_{x_i \in C_j}x_i$$
where $j$ is the $j$-th cluster
We then place each centroid (center of each cluster) at their corresponding means, reassign all examples to the cluster it is now closest to, recalculate the means, and continue repeating until convergence. Our goal is to minimize our cost function $J$:
$$J(C, \mu) = \sum_{j=1}^k \sum_{x_i \in C_j} \Vert x_i - \mu_j \Vert ^2$$
as this represents the distance between each example and the mean of the cluster they belong to. Once we have this as low as possible between all examples then we have converged and found the clusters that group pieces of data together.
Remember, all we're trying to do is find groupings within the data. If you still don't fully understand the math and/or concept, skip down to the example section to really understand the purpose.
Given a set of unlabeled data ${x_1, \ldots, x_n}$ and parameter $K$, the $K$-Means Clustering algorithm works like this:
You have unlabeled data with two features. The two features are stance on progressive taxes and stance on government controlled healthcare (on a scale of 1-6), i.e. $x_8 = (3,5)$ means the 8th person feels pretty neutral about progressive tax and strongly about government controlled healthcare.
The unlabeled data presents nothing useful to you so you run $K$-Means to hopefully learn some structure from your data. The training data from 6 different people is presented below:
$$x_1 = (0,0)$$
$$x_2 = (1,1)$$
$$x_3 = (1,2)$$
$$x_4 = (4,3)$$
$$x_5 = (3,4)$$
$$x_6 = (6,6)$$
Running the $K$-means Clustering algorithm, we want to assign data to a set of clusters. We don't know how any of them are related (labels) but once we find a structure between them after grouping, we can then do more digging to understand our data.
Goal is to assign each example $x_1, \ldots, x_n$ to one of the $K$-Clusters $C_1, \ldots, C_k$.
So first, we initialize the clusters at randoms spots and assign each example to the closest cluster. We set $K$$=2$, so our two clusters are:
$$C_1 = (4,5)$$
$$C_2 = (5,4)$$
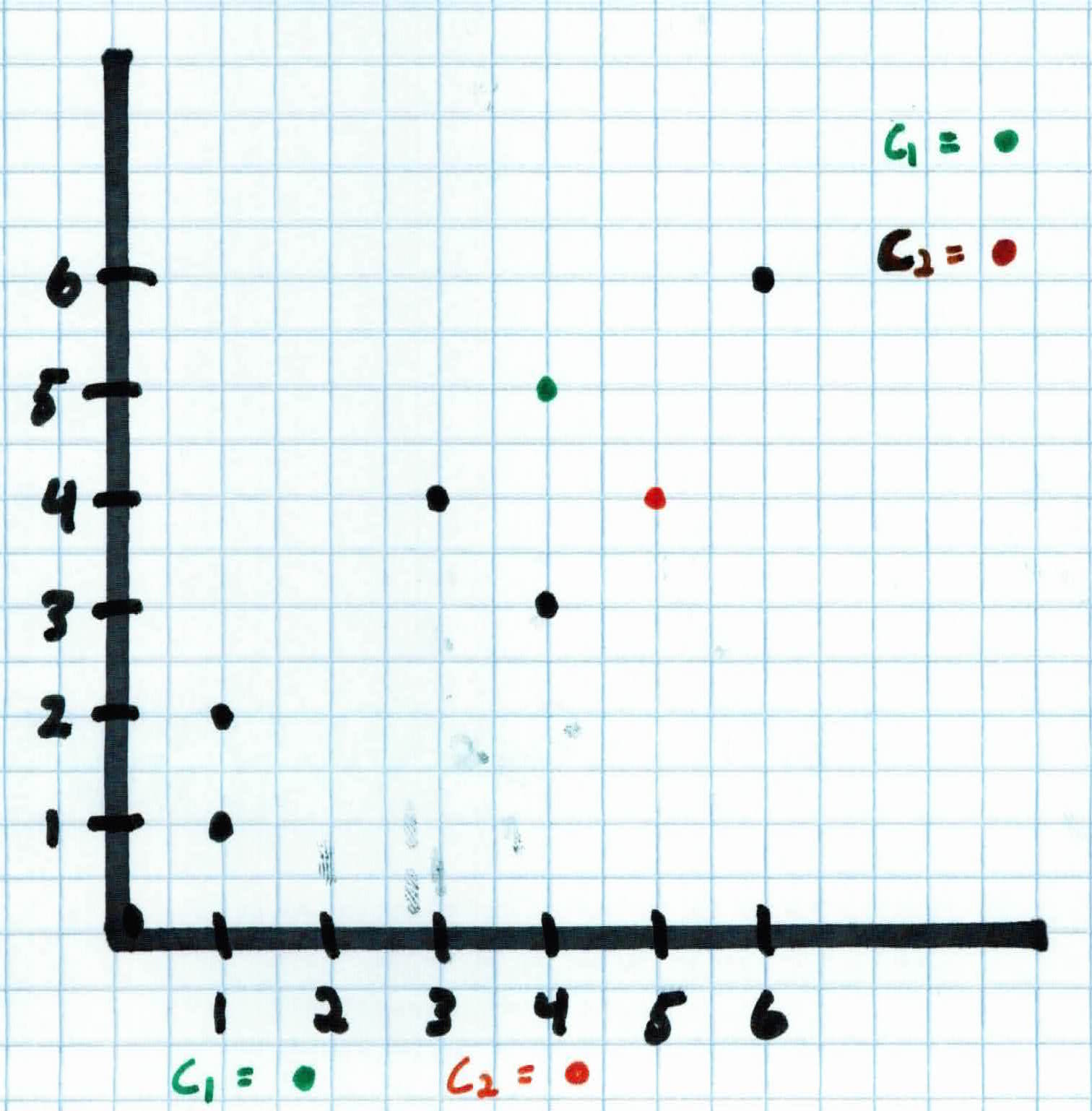
For each example $x_i$, we calculate the euclidean distance to each cluster and assign each example to the nearest cluster. So, for the first person who fully believes in a flat tax and that healthcare should be privatized $x_1 = (0,0)$, we get:
$$d(x_1, C_1) = \sqrt{(0-4)^2+(0-5)^2} = \sqrt{41}$$
$$d(x_1, C_2) = \sqrt{(0-5)^2+(0-5)^2} = \sqrt{50}$$
Therefore, person 1 will be assigned to $C_1$ since it's closest to that. After doing the calculations for the rest of the examples, we see that $x_1, x_2, x_3, x_5$ will be assigned to $C_1$ and $x_4 , x_6$ to $C_2$.
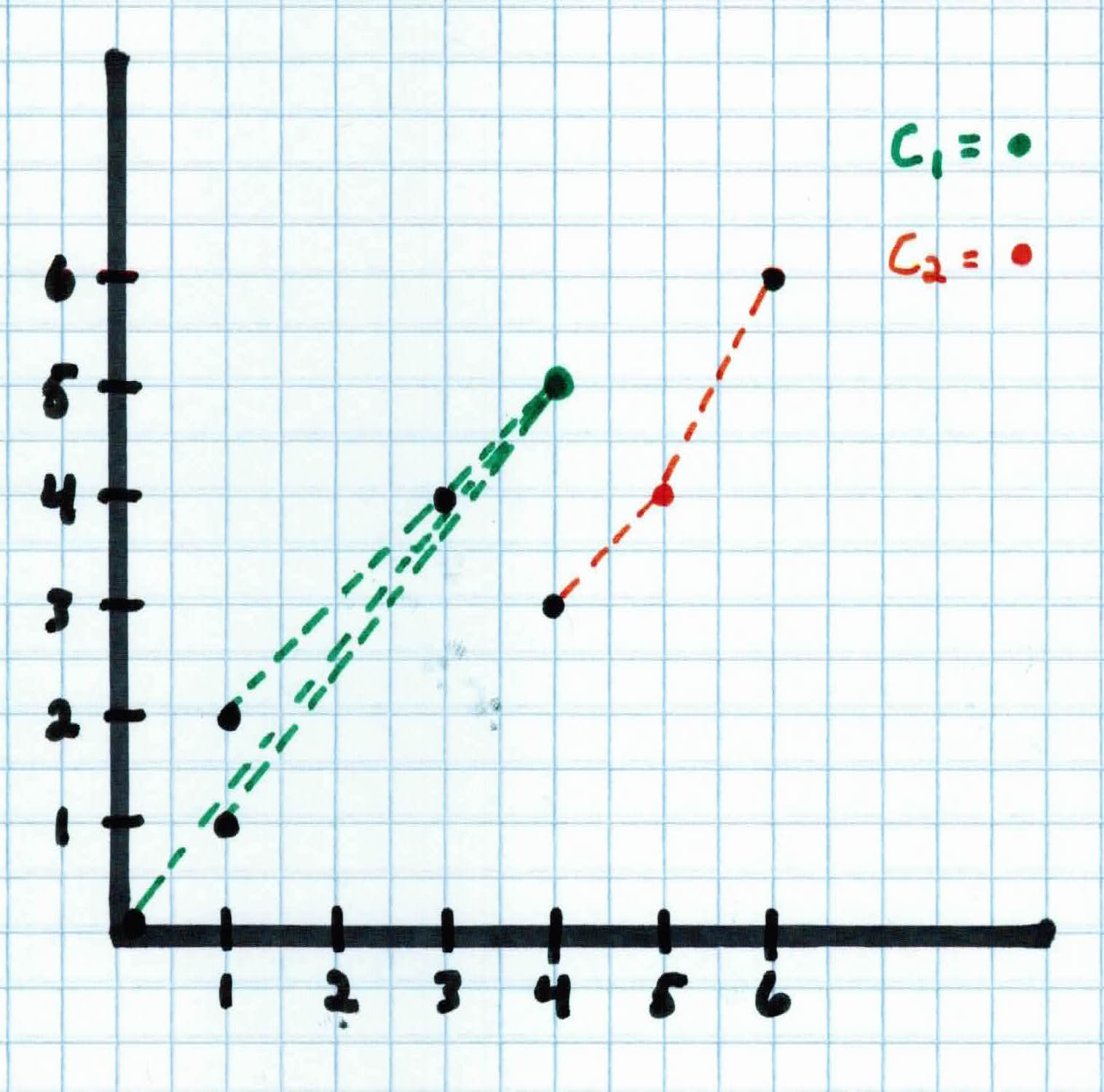
Once each example is assigned to a cluster, you can then calculate the mean for each cluster with:
$$\mu_j = \frac{1}{\mid C_j \mid}\sum_{x_i \in C_j}x_i$$
$$\mu_{1,x} = \frac{1}{4} (0+1+1+3) = 1$$
$$\mu_{1,y} = \frac{1}{4} (0+1+2+4) = \frac{7}{4}$$
$$\mu_{2,x} = \frac{1}{2} (4+6) = 5$$
$$\mu_{2,y} = \frac{1}{2} (3+6) = 4.5$$
Then place the center of each cluster at their respective means, i.e. $C_1$ will be at $(1, \frac{7}{4})$ and $C_2$ will be placed at $(5, 4.5)$.
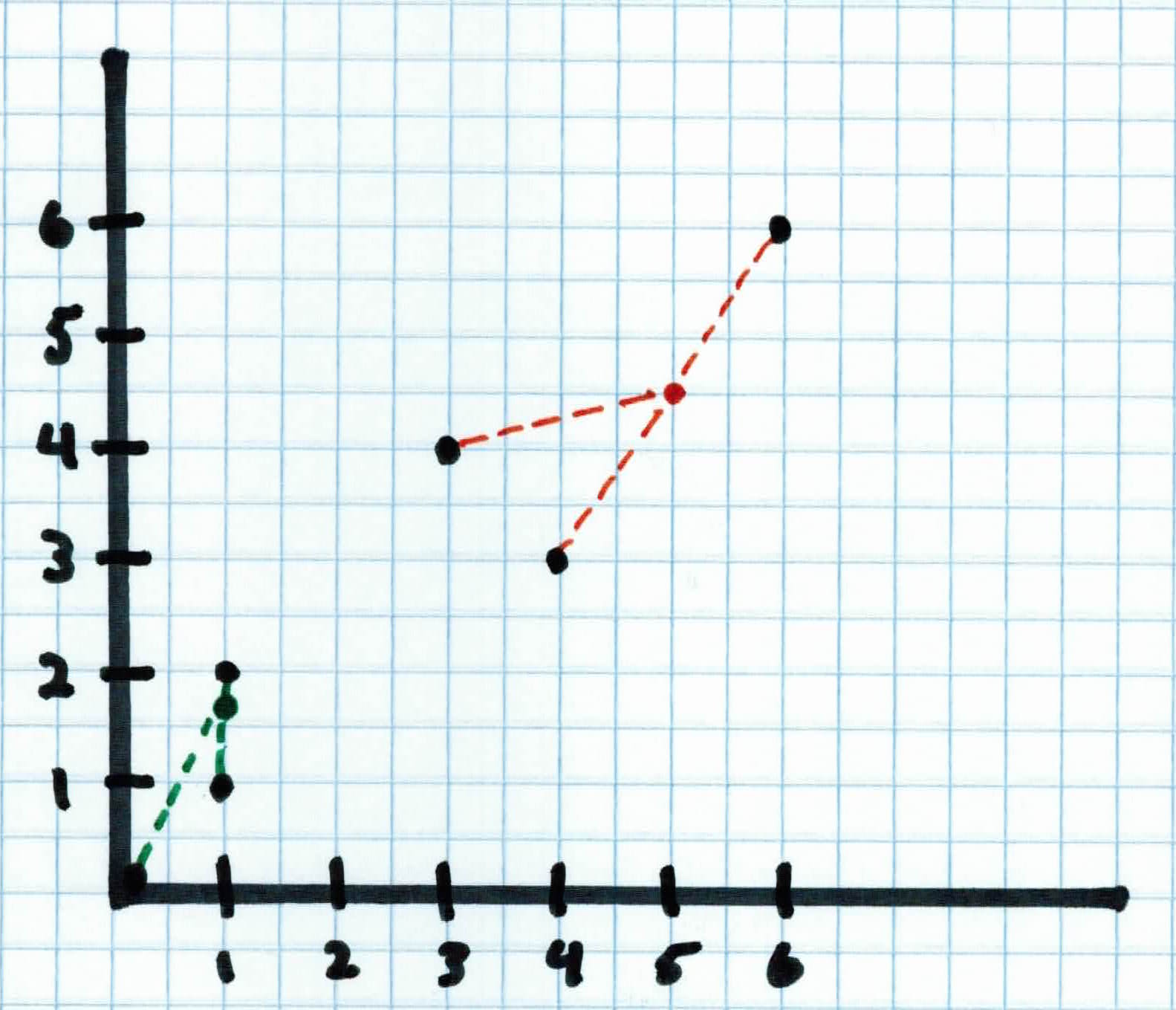
This process repeats until convergence. Convergence could mean that the clusters no longer move, being placed at the most optimal spot, or it has reached a max number of iterations set by the user.
At convergence, our clusters have found structure within our data. After observing the data and the clusters, we see that the people that belong to $C_1$ are mostly republican and the people that belong to $C_2$ are mostly democrat. We found this out without knowing what to look for.
Now, you might be thinking, Couldn't you have just seen the plotting of the data and know to group them together?. The answer to that is yes. But, when we go to more complicated data with higher dimensions, seeing the data won't work and $K$-Means still will. This simple example was just for illustration purposes.
$K$-Means is an unsupervised learning algorithm, meaning it has no labels provided and one must learn to find structure by clustering the data. $K$-Means is easy to implement and works well when you have data centered around means. Unfortunately, there is no theoretical foundation, you need to know parameter $K$, and similar to $K$NN, it could also suffer from the curse of dimensionality.
In $K$-Means, all you simply do is randomly place $K$ centroids in your data. You then assign each example to the centroid it is closest to, to form $K$ clusters. The next step is to calculate the mean of each cluster and move the corresponding centroid to its mean. These steps repeat until convergence. Other observations: